
����Ŀ�����壺��һ��Խ���ֱ�ǵ��ı��ν��������Ρ����������ڱߣ����ظ�����ȵ��ı��ν��������Ρ�����ͼ�٣����ı���ABCD�У�����A����C��90�������ı���ABCD�ǡ����Ρ�����ͼ�ڣ����ı���ABCD�У���AB��AD��BC��DC�����ı���ABCD�ǡ����Ρ���
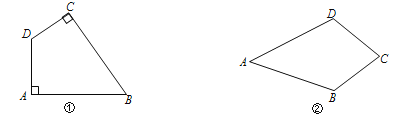
��1����ͼ���ڱ߳�Ϊ1�������������У�A��B��C�ڸ�㣨С�����εĶ��㣩�ϣ���ֱ���ͼ�ۡ�ͼ���л��������Ρ�ABCD�͡����Ρ�ABCD������Ҫ��D��D���ڸ���ϣ���
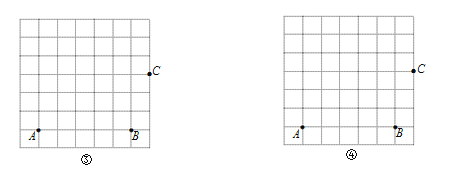
��2������˵����ȷ���� ������д������ȷ���۵���ţ�
��һ��Ա�ƽ�еġ����Ρ��Ǿ��Σ���һ��Ա���ȵġ����Ρ��Ǿ��Σ�
��һ��Ա���ȵġ����Ρ������Σ���һ��Ա�ƽ�еġ����Ρ������Σ�
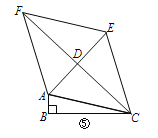
��3����ͼ�����ڡ�ABC�У���ABC��90������ACΪһ�������������Ρ�ACEF����AC��EC��AF��EF��AE��CF���ڵ�D��
������ACE����AFE����֤�������Ρ�ACEF�����Σ�
�������������£�����BD����BD��![]() ����ACB��15������ACD��30������ֱ��д���ı���ACEF�������
����ACB��15������ACD��30������ֱ��д���ı���ACEF�������
���𰸡���1������������2���٢ڢۢ�����3����֤������������![]()
��������
��1���������κ����ε��ص㻭ͼ���ɣ�
��2�����ݾ��ε��ж����������ε��ж�����������κ����ε����ʶ�ÿһ��ѡ������ƶϼ��ɣ�
��3�����ȸ�����֪�ó���ACF�ա�ECF���ٽ�ϡ�ACE����AFE���Ƴ�AC��EF��AF��CE����֤��������ACEF��ƽ���ı��Σ�����ΪAC��EC���ɵó�����ACEF�����Σ�
��ȡAC���е�M������BM��DM�������ı���ACEF�����οɵ�A��B��C��D�ĵ㹲Բ����M��Բ�ģ�����Բ�ܽǶ������Ƴ���BMD=90�㣬�������AC���ٸ��ݡ�ACD��30���������AD��CD�ij������������ε������
��1��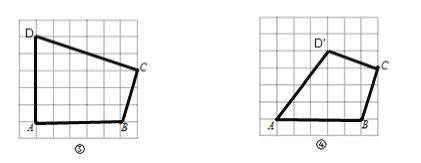 ��
��
��2������Ϊ��A����C��90�������һ��Ա�ƽ�п����ж��ı���Ϊ���Σ��ʢ���ȷ��
����Ϊ��A����C��90�������һ��Ա���ȿ����ж��ı���Ϊ���Σ��ʢ���ȷ��
����ΪAB��AD��BC��DC�����һ��Ա���ȿ����ж��ı���Ϊ���Σ��ʢ���ȷ��
����ΪAB��AD��BC��DC�����һ��Ա�ƽ�п����ж��ı���Ϊ���Σ��ʢ���ȷ��
�ʴ�Ϊ���٢ڢۢ���
��3����֤������AC��EC��AF��EF��CF��CF��
���ACF�ա�ECF��SSS����
���ACF����ECF����AFC����EFC��
�ߡ�ACE����AFE��
���ACF����EFC����ECF����AFC��
��AC��EF��AF��CE��
������ACEF��ƽ���ı��Σ�
��AC��EC��
������ACEF������
����ͼ��ȡAC���е�M������BM��DM��
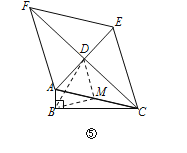
���ı���ACEF�����Σ�
��AE��CF����ADC=90�㣬
�֡ߡ�ABC=90�㣬
��A��B��C��D�ĵ㹲Բ����M��Բ�ģ�
�ߡ�ACB=15�㣬
���AMB=30�㣬
�ߡ�ACD=30����
���AMD=60�㣬
���BMD=90�㣬
���BMD�ǵ���ֱ�������Σ�
��BM=DM=![]() BD=
BD=![]() ��
��![]() =1��
=1��
��AC=2��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룩��
��AD=AC��sin30��=1��CD=AC��cos30��=![]() ��
��
������ACEF�����=![]() ��1��
��1��![]() ��4=
��4=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���ö�ά�����ѧ��ѧ��ͳһ���ţ���ɫС�����α�ʾ1����ɫС�����α�ʾ0����ÿһ�����ִ��������μ�Ϊa��b��c��d����ô���ù�ʽa��23-b��22-c��21+d�����ÿһ�е����ݣ���һ�б�ʾ�꼶���ڶ��б�ʾ�༶����ͼ1��ʾ����һ�����ִ�������������1��0��0��1�����ʾ������Ϊ1��23+0��22+0��21+1=9������09���ڶ������ִ�������������1��0��1��0�����ʾ������Ϊ1��23+0��22+1��21=10������10���Դ����ƣ�ͼ1������ͳһѧ��Ϊ091034����ʾ9�꼶10��34�ţ�С������Ӧ�Ķ�ά����ͼ2��ʾ�������ı����_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy��![]() ��ͼ
��ͼ![]() ����֪������
����֪������![]() ��������
��������![]() ��
��![]() ��
��

![]() ��������߶���C�����ꣻ
��������߶���C�����ꣻ
![]() ����AC��y���ڵ�D������BD��BC������C��
����AC��y���ڵ�D������BD��BC������C��![]() ������Ϊ��H�������߶Գ��ύx����G������HG����HG�ij���
������Ϊ��H�������߶Գ��ύx����G������HG����HG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
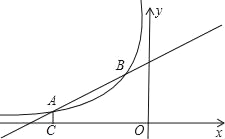
����Ŀ����ͼ����֪��A����4��a����B����1��2����һ�κ���y1=kx+b�뷴��������![]() ��m��0��ͼ����������㣬AC��x����C��
��m��0��ͼ����������㣬AC��x����C��
��1����һ�κ����ͷ����������Ľ���ʽ��
��2����P��ֱ��AB�ϵ�һ�㣬����PC������PCA���������![]() �����P�����꣮
�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�����֪��|a|�ļ�������������������a��Ӧ�ĵ���ԭ��ľ��룬��|a|��|a��0|��Ҳ����˵��|a|��ʾ����������a����0��Ӧ��֮��ľ��룮������ۿ����ƹ�Ϊ��|a��b|��ʾ����������a��b��Ӧ��֮��ľ��룮
��1����֪|a|��2����a��ֵ��
�⣺����������ԭ�����Ϊ2�ĵ�Ķ�Ӧ��Ϊ��2��2����a��ֵΪ2�ͩ�2��
��2����֪|a��1|��2����a��ֵ��
�⣺����������1�ľ���Ϊ2��Ķ�Ӧ��Ϊ3�ͩ�1����a��ֵΪ3�ͩ�1��
�����Ķ����ϵĽⷨ������������⣺
��1����֪|a|��![]() ����a��ֵ��
����a��ֵ��
��2����֪|a+2|��4����a��ֵ��
��3���������ϱ�ʾa�ĵ��ک�4��2֮�䣬��|a+4|+|a��2|��ֵΪ������
��4����a��������ʱ����|a+4|+|a��2|��ֵ��С����Сֵ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ����ֵ������֪����|a|��ʾ��a�������ϵĶ�Ӧ����ԭ��ľ��룮�磺|5|��ʾ5�������ϵĶ�Ӧ�㵽ԭ��ľ��룮��|5|=|5��0|����|5��0|��ʾ5��0�������϶�Ӧ������֮��ľ��룮���Ƶģ��У�|5��3|��ʾ5��3�������϶�Ӧ������֮��ľ��룻|5+3|=|5������3��|������|5+3|��ʾ5����3�������϶�Ӧ������֮��ľ��룮һ��أ���A��B�������Ϸֱ��ʾ������a��b����ôA��B֮��ľ���ɱ�ʾΪ|a��b|��
����ݾ���ֵ�����岢����������������⣺
��1����һ�����ᡣ���������Ϸֱ���A��B��ʾ��1��3������
��2�������ϱ�ʾ1��3������֮��ľ������� ����
��3����A��B��C�������Ϸֱ��ʾ������1��3��x����ôC��A�ľ�����C��B�ľ���֮�Ϳɱ�ʾΪ�� ���ú�����ֵ��ʽ�ӱ�ʾ��
��4�����������۵���ʹ�ñ�ʾ1��3�������غϣ���ԭ�����ʾ�� �ĵ��غ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵĵ�A�͵�B֮��ľ���Ϊ32����λ���ȣ���A��ԭ�����ߣ�����ԭ��5����λ���ȣ���B��ԭ����ұߡ�
(1)��A����Ӧ������___����B��Ӧ������___��
(2)����֪�������ϵĵ�E�ӵ�A���������˶����ٶ�Ϊÿ��2����λ���ȣ�ͬʱ��F�ӵ�B���������˶����ٶ�Ϊÿ��4����λ���ȣ��ڵ�C����F���˵�E�����C��Ӧ������
(3)����֪�������ϵĵ�M�ӵ�A���������˶�,�ٶ�Ϊÿ��2����λ����,ͬʱ��N�ӵ�B���������˶�,�ٶ�Ϊÿ��4����λ����,���߶�NO���е�ΪP(Oԭ��)�����˶��������߶�POAM��ֵ�Ƿ�仯?�����䣬����ֵ�����仯����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
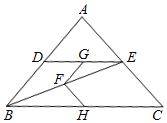
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����D�DZ�AB�ĵ㣬DE��BC��AC�ڵ�E������BE����F��G��H�ֱ�ΪBE��DE��BC���е㣮
��1����֤��FG��FH��
��2������AΪ���ٶ�ʱ��FG��FH����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϲ�����й����⣺����֪��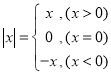 �����Ե�
�����Ե�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ���������ǿ������������������������⣺
���������ǿ������������������������⣺
��1����֪![]() ��
��![]() ��������,��
��������,��![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2����֪![]() ��
��![]() ��
��![]() ������������
������������![]() ����
����![]() ��ֵ��
��ֵ��
��3����֪![]() ��
��![]() ��
��![]() ����������
����������![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com