
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.

 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx的图象过点 (2,0),(-1,6).
(1)求二次函数的关系式;
(2)写出它的对称轴和顶点坐标;
(3)请说明x在什么范围内取值时,函数值y<0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:
![]()
(1)从中2张卡片,使这2张卡片上数字的乘积最大,如何抽取,最大值是多少?
(2)从中抽取2张卡片,使这两张卡片数相除的商最小,如何抽取,最小值是多少?
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子.(要写出两种运算式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为
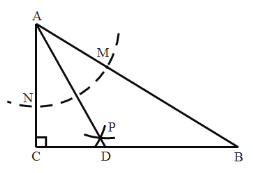
①![]() 是
是![]() 的平分线;
的平分线;
②若![]() ,则
,则![]() ;
;
③![]() ;
;
④点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1)、B(0,﹣2)、C(1,0),点P(0,2)绕点A旋转180°得到点![]() ,点
,点![]() 绕点B旋转180°得到点
绕点B旋转180°得到点![]() ,点
,点![]() 绕点C旋转180°得到点
绕点C旋转180°得到点![]() ,点
,点![]() 绕点A旋转180°得到点
绕点A旋转180°得到点![]() ,…,按此作法进行下去,则点
,…,按此作法进行下去,则点![]() 的坐标为( )
的坐标为( )
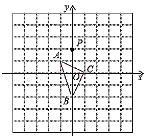
A.(0,4)B.(﹣2,0)C.(2,﹣4)D.(﹣2,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
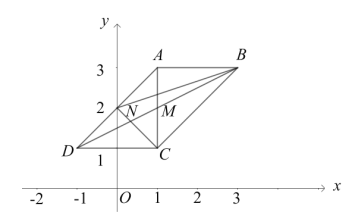
【题目】如图,平行四边形ABCD的两个顶点坐标分别为A(1,3),B(3,3),对角线的交点为M(1,2),AD与y轴的交点为N.
(1)求C、D点的坐标;
(2)求证:△BCN的面积是平行四边形ABCD面积的一半;
(3)除了点N,坐标轴上是否存在点P,使△BCP的面积是平行四边形ABCD面积的一半,若存在,直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下
+1,给出定义如下
我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)
(1)通过计算判断数对“﹣2,1”,“4,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m” “共生有理数对”(填“是”或“不是”),并说明理由;
(4)若(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() 的图象上,点D的坐标为
的图象上,点D的坐标为![]() .将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
.将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
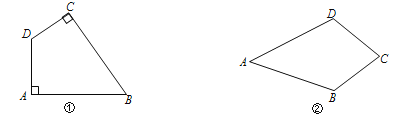
(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);
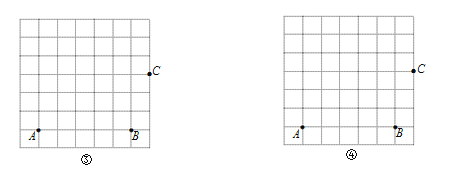
(2)下列说法正确的有 ;(填写所有正确结论的序号)
①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
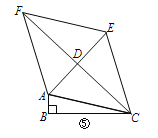
(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.
①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com