
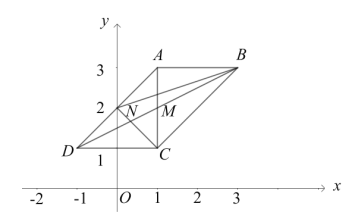
【题目】如图,平行四边形ABCD的两个顶点坐标分别为A(1,3),B(3,3),对角线的交点为M(1,2),AD与y轴的交点为N.
(1)求C、D点的坐标;
(2)求证:△BCN的面积是平行四边形ABCD面积的一半;
(3)除了点N,坐标轴上是否存在点P,使△BCP的面积是平行四边形ABCD面积的一半,若存在,直接写出P点的坐标;若不存在,请说明理由.
【答案】(1) C(1,1),D(-1,1);(2)见解析.(3) P点的坐标为(-2,0),(2,0)或(0,-2)
【解析】
(1)根据平行四边形的性质求出C,D两点的坐标;
(2)分别表示出△BCN的面积,平行四边形ABCD的面积,然后探究他们之间的大小关系;
(3)分三种情况进行分类讨论,P在y负半轴,在x正半轴,x负半轴分别进行讨论.
解:(1)∵A(1,3),B(3,3), M(1,2),
∴AB=2,AM=1,AB![]() x轴,AM⊥x轴,
x轴,AM⊥x轴,
∴A,C,M三点的横坐标相等为1,C,D两点的纵坐标相等.
∵四边形ABCD是平行四边形,M是平行四边形对角线的交点,
∴CD=AB=2,CD![]() AB,AM=CM=1
AB,AM=CM=1
∴C点的纵坐标为3-2=1,D点的横坐标为-1
∴C(1,1),D(-1,1).
(2)设A点到BC的距离为h,则平行四边形ABCD的面积为AB![]() h.
h.
∵四边形ABCD是平行四边形,
∴AD![]() BC
BC
∴点N到BC的距离为h
∴△BCN的面积为![]() BC
BC![]() h
h
∴△BCN的面积是平行四边形ABCD面积的一半.
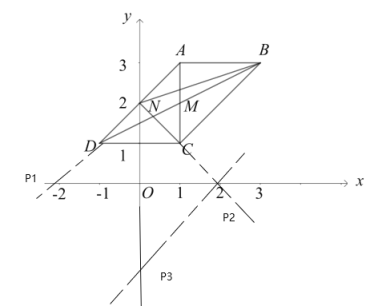
(3)根据平行线之间的距离相等,则延长AD交x轴与P1,有△BCP1的面积是平行四边形ABCD面积的一半.
设直线AD的解析式为y=kx+b,将A(1,3),D(-1,1)代入y=kx+b中,得
![]() 解得
解得![]()
∴直线AD的解析式为y=x+2
∴∠ADC=45°
当y=0时,x=-2
∴P1(-2,0)
当x=0时,y=2
∴N(0,2)
又∵C(1,1),D(-1,1),
∴NC=ND
∴∠NCD=∠ADC=45°
∴三角形NDC为等腰直角三角形,∠DNC=90°,∠ONC=45°
延长NC交x轴于点P2,则三角形NOP2是等腰直角三角形,所以OP2=ON=2
∴P2(2,0)
过P2作AD的平行线交y轴于P3,则P2 P3的解析式为y=x-2.
当x=0时,y=-2.
∴P3(0,-2)
则P点的坐标为(-2,0),(2,0)或(0,-2)时,△BCP的面积是平行四边形ABCD面积的一半.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】△ABC和△DEF的顶点A与D重合,已知∠B=90°,∠BAC=30°,BC=6,∠FDE=90°,DF=DE=4.
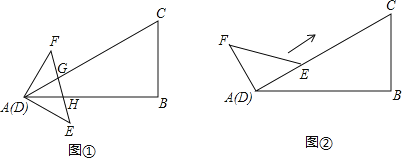
(1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH.设![]() ,在射线DF上取一点P,记:
,在射线DF上取一点P,记: ![]() ,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
(2)在(1)的条件下,求当x为何值时PC//AB;
(3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动![]() 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则二次函数
,则二次函数![]() 的图象与坐标轴的公共点的个数是2或3.
的图象与坐标轴的公共点的个数是2或3.
其中正确的是![]()
A. 只有![]() B. 只有
B. 只有![]() C. 只有
C. 只有![]() D. 只有
D. 只有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
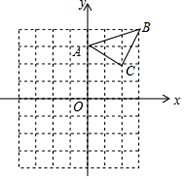
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC绕点O逆时针旋转90°后的△A1B1C1.
(2)将△ABC向右平移3个单位,作出平移后的△A2B2C2.
(3)若点M是平面直角坐标系中直线AB上的一个动点,点N是x轴上的一个动点,且以O、A2、M、N为顶点的四边形是平行四边形,请直接写出点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离.而|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离.类似的,有:|5﹣3|表示5、3在数轴上对应的两点之间的距离;|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
请根据绝对值的意义并结合数轴解答下列问题:
(1)画一条数轴。并在数轴上分别用A、B表示出1和3的两点
(2)数轴上表示1和3的两点之间的距离是 ;
(3)点A、B、C在数轴上分别表示有理数1、3、x,那么C到A的距离与C到B的距离之和可表示为 (用含绝对值的式子表示)
(4)若将数轴折叠,使得表示1和3的两点重合,则原点与表示数 的点重合
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com