
【题目】△ABC和△DEF的顶点A与D重合,已知∠B=90°,∠BAC=30°,BC=6,∠FDE=90°,DF=DE=4.
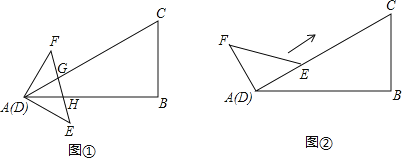
(1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH.设![]() ,在射线DF上取一点P,记:
,在射线DF上取一点P,记: ![]() ,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
(2)在(1)的条件下,求当x为何值时PC//AB;
(3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动![]() 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 移动到AD=
移动到AD=![]() 时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
【解析】试题分析:(1)首先证明△DFG≌△DEH(SAS),进而得出∠FDG=∠EDH,进而得出DF=|![]() |=x|
|=x|![]() |=x|
|=x|![]() |=4x,在Rt△DPH中,∠FDG=30°,可得PH′=
|=4x,在Rt△DPH中,∠FDG=30°,可得PH′=![]() DP=2x,由y=S△PDC=
DP=2x,由y=S△PDC=![]() DCPH′求出即可;
DCPH′求出即可;
(2)由(1)知∠FDG=30°,得出∠FDG=∠DCP,以及DP=PC若PH⊥AB则M是DC的中点DM=6,在Rt△DPH中,∠FDG=30°,利用cos∠FDG=![]() 求出AP的长,进而得出x的值;
求出AP的长,进而得出x的值;
(3)分别利用线段AD、FC、BC的长为斜边时求出符合条件的值即可.
试题解析:(1)如图①,过P作PH′⊥AC于H′.
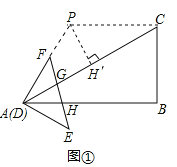
∵DF=DE,
∴∠DFE=∠E
又∵FG=EH,
在△DFG和△DEH中
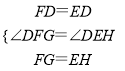 ,
,
∴△DFG≌△DEH(SAS),
∴∠FDG=∠EDH,
∵∠FDE=90°,且∠FDE=∠FDG+∠EDH+∠BAC
∵∠BAC=30°,
∴∠FDG=30°,
∵DF=4,
∴|![]() |=4
|=4
∵![]() =x
=x![]() =x
=x![]() ,
,
∴DP=|![]() |=x|
|=x|![]() |=x|
|=x|![]() |=4x,
|=4x,
在Rt△DPH中,∠FDG=30°,
∴PH′=![]() DP=2x,
DP=2x,
∠B=90°,∠BAC=30°,BC=6,
∴AC=CD=12,
y=S△PDC=![]() DCPH′=
DCPH′=![]() ×122x=12x(x>0);
×122x=12x(x>0);
(2)∵PC∥AB,
∴∠BAC=∠DCP
∵∠BAC=30°,
∴∠DCP=30°,
由(1)知∠FDG=30°,
∴∠FDG=∠DCP,
∴DP=PC
若PH⊥AB,则M是DC的中点DM=6,
在Rt△DPH中,∠FDG=30°,
cos∠FDG=![]() =
=![]() =
=![]() ,
,
∴AP=4![]() ,
,
DP=AP=4x,
∴x=![]() ;
;
(3)如图②,
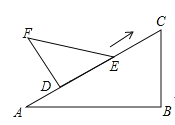
设AD=t,DC=12-t(0<t<12)
FC2=DF2+DC2=42+(12-t)2,
①AD2=FC2+BC2
t2=42+(12-t)2+36
解得:t=![]() (FC至少等于4,故不合题意,舍去)
(FC至少等于4,故不合题意,舍去)
②BC2=FC2+AD2
36=42+(12-t)2+t2,无解,
③FC2=BC2+AD2
∴42+(12-t)2=36+t2
解得t=![]() ,
,
∴当△DEF移动到AD=![]() 时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“迷你三点矩形”.
如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“迷你三点矩形”.
如图2,已知M(4,1),N(-2,3),点P(m,n).
(1)①若m=1,n=4,则点M,N,P的“迷你三点矩形”的周长为 ,面积为 ;
②若m=1,点M,N,P的“迷你三点矩形”的面积为24,求n的值;
(2)若点P在直线y=-2x+4上.当点M,N,P的“迷你三点矩形”为正方形时,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
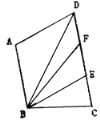
【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°,∠DBF=14°,∠ADC的度数为_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:
![]()
(1)从中2张卡片,使这2张卡片上数字的乘积最大,如何抽取,最大值是多少?
(2)从中抽取2张卡片,使这两张卡片数相除的商最小,如何抽取,最小值是多少?
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子.(要写出两种运算式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
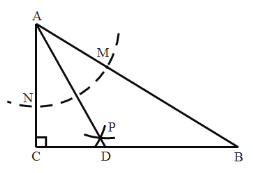
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为
①![]() 是
是![]() 的平分线;
的平分线;
②若![]() ,则
,则![]() ;
;
③![]() ;
;
④点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
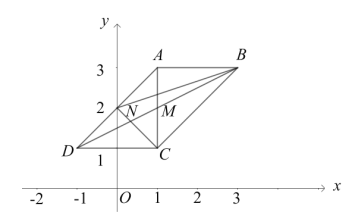
【题目】如图,平行四边形ABCD的两个顶点坐标分别为A(1,3),B(3,3),对角线的交点为M(1,2),AD与y轴的交点为N.
(1)求C、D点的坐标;
(2)求证:△BCN的面积是平行四边形ABCD面积的一半;
(3)除了点N,坐标轴上是否存在点P,使△BCP的面积是平行四边形ABCD面积的一半,若存在,直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com