练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（﹣1，1）、B（0，﹣2）、C（1，0），点P（0，2）绕点A旋转180°得到点，点绕点B旋转180°得到点，点绕点C旋转180°得到点，点绕点A旋转180°得到点，…，按此作法进行下去，则点的坐标为( )

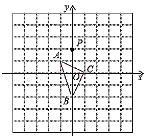
    A.（0，4）B.（﹣2，0）C.（2，﹣4）D.（﹣2，﹣2）

    【答案】D

    【解析】

    画出P1～P6，寻找规律后即可解决问题．

    解：如图所示，P1（-2，0），P2（2，-4），P3（0，4），P4（-2，-2），P5（2，-2），P6（0，2），发现6次一个循环，


    ∵2020÷6=336…4，
    ∴点P2020的坐标与P4的坐标相同，即P2020（-2，-2），
    故答案为D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有理数a、b、c在数轴上的位置如图所示．

    （1）化简：|a|＝　 　|b|＝　 　；

    （2）比较大小a﹣c　 　0，a+b　 　0．

    （3）将a，b，c，﹣a，﹣b，﹣c按从小到大的顺序，用“＜”号连接．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年4月23日，是第25个世界读书日．为了解学生每周阅读时间，某校随机抽取了部分学生进行调查，根据调查结果，将阅读时间x（单位：小时）分成了4组，A：0≤x＜2；B：2≤x＜4；C：4≤x＜6；D：6≤x＜8，试结合图中所给信息解答下列问题：

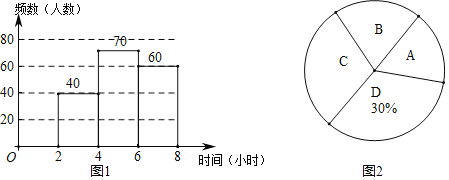
    （1）这次随机抽取了　 　名学生进行调查；扇形统计图中，扇形B的圆心角的度数为　 　．

    （2）补全频数分布直方图；

    （3）若该校共有2000名学生，试估计每周阅读时间不少于4小时的学生共有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某自行车厂计划一周生产自行车2100辆，平均每天计制生产300辆，实际每天生产量与计划量相比有出入，下表是某周的生产情况.（超过每天计划生产数记为正，不足每天计划生产数记为负）

    星期

    一

    二

    三

    四

    五

    六

    日

    每天超出计划的量数

    （1）该厂星期四实际生产自行车______辆

    （2）该厂本周实际每天平均生产多少辆自行车?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是半径为3的⊙O上的点，

    尺规作图：作⊙O的内接正六边形ABCDEF；

    求中弧AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校利用二维码进行学生学号统一编排．黑色小正方形表示1，白色小正方形表示0，将每一行数字从左到右依次记为a，b，c，d，那么利用公式a×23-b×22-c×21+d计算出每一行的数据．第一行表示年级，第二行表示班级，如图1所示，第一行数字从左往右依次是1，0，0，1，则表示的数据为1×23+0×22+0×21+1=9，计作09，第二行数字从左往右依次是1，0，1，0，则表示的数据为1×23+0×22+1×21=10，计作10，以此类推，图1代表的统一学号为091034，表示9年级10班34号．小明所对应的二维码如图2所示，则他的编号是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（概念学习）

    规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”，一般地，把 （a≠0）记作a，读作“a的圈n次方”．

    （1）（初步探究）

    直接写出计算结果：2③=_______，（-）⑤=_______；

    （2）（深入思考）

    我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？

    Ⅰ.试一试：仿照上面的算式，将下列运算结果直接写成幂的形式．

    （﹣3）④=_______；5⑥=_______； (-) ⑩=_______．

    Ⅱ. 想一想：将一个非零有理数a的圈n次方写成幂的形式等于_______；

    Ⅲ. 算一算：

    12÷(-)④×(-2)⑤－(-)⑥÷3.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

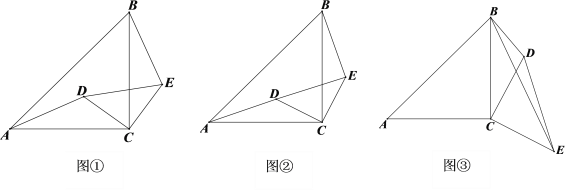
    【题目】如图①已知△ACB和△DCE为等腰直角三角形，按如图的位置摆放，直角顶点

    C重合．

    （1）求证：AD=BE；

    （2）将△DCE绕点C旋转得到图②，点A、D、E在同一直线上时，若CD=,BE=3，

    求AB 的长；

    （3）将△DCE绕点C顺时针旋转得到图③，若∠CBD=45°，AC=6，BD=3，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：我们知道|a|的几何意义是在数轴上数a对应的点与原点的距离，即|a|＝|a﹣0|，也就是说，|a|表示在数轴上数a与数0对应点之间的距离．这个结论可以推广为：|a﹣b|表示在数轴上数a与b对应点之间的距离．

    例1　已知|a|＝2，求a的值．

    解：在数轴上与原点距离为2的点的对应数为﹣2和2，即a的值为2和﹣2．

    例2　已知|a﹣1|＝2，求a的值．

    解：在数轴上与1的距离为2点的对应数为3和﹣1，即a的值为3和﹣1．

    仿照阅读材料的解法，解决下列问题：

    （1）已知|a|＝，求a的值；

    （2）已知|a+2|＝4，求a的值；

    （3）若数轴上表示a的点在﹣4与2之间，则|a+4|+|a﹣2|的值为　　；

    （4）当a满足　　时，则|a+4|+|a﹣2|的值最小，最小值是　　．

    查看答案和解析>>

    同步练习册答案