
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下
+1,给出定义如下
我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)
(1)通过计算判断数对“﹣2,1”,“4,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m” “共生有理数对”(填“是”或“不是”),并说明理由;
(4)若(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.
【答案】解:(﹣2,1)不是“共生有理数对”;(4,![]() )是共生有理数对;(2)a=
)是共生有理数对;(2)a=![]() ;(3)是. (4)
;(3)是. (4)![]()
【解析】
(1)计算后,根据“共生有理数对”的定义即可判断;
(2)根据“共生有理数对”的定义可得:6-a=6a+1,即可求得a的值;
(3)根据(m,n)是“共生有理数对”可得:m-n=mn+1,再根据“共生有理数对”的定义即可判断;
(4)根据“共生有理数对”的定义即可解决问题.
解:(1)﹣2﹣1=﹣3,﹣2×1+1=1,
∴﹣2﹣1≠﹣2×1+1,
∴(﹣2,1)不是“共生有理数对”;
∵4﹣![]() =
=![]() ,
,![]() ,
,
∴(4,![]() )是共生有理数对;
)是共生有理数对;
(2)由题意得:
6﹣a=6a+1,
解得a=![]() ;
;
(3)是.
理由:﹣n﹣(﹣m)=﹣n+m,
﹣n(﹣m)+1=mn+1,
∵(m,n)是“共生有理数对”,
∴m﹣n=mn+1,
∴﹣n+m=mn+1,
∴(﹣n,﹣m)是“共生有理数对”;
故答案为:是;
(4)∵(m,n)是“共生有理数对”,
∴m﹣n=mn+1,
即mn﹣m=﹣(n+1),
∴(n﹣1)m=﹣(n+1),
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每天超出计划的量数 |
|
|
|
|
|
|
|
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把 ![]() (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.
(1)(初步探究)
直接写出计算结果:2③=_______,(-![]() )⑤=_______;
)⑤=_______;
(2)(深入思考)
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
Ⅰ.试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(﹣3)④=_______;5⑥=_______; (-![]() ) ⑩=_______.
) ⑩=_______.
Ⅱ. 想一想:将一个非零有理数a的圈n次方写成幂的形式等于_______;
Ⅲ. 算一算:
12÷(-![]() )④×(-2)⑤-(-
)④×(-2)⑤-(-![]() )⑥÷3.
)⑥÷3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
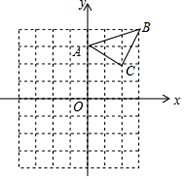
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
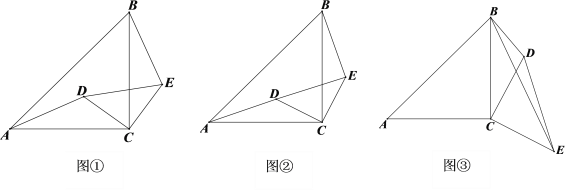
【题目】如图①已知△ACB和△DCE为等腰直角三角形,按如图的位置摆放,直角顶点
C重合.
(1)求证:AD=BE;
(2)将△DCE绕点C旋转得到图②,点A、D、E在同一直线上时,若CD=![]() ,BE=3,
,BE=3,
求AB 的长;
(3)将△DCE绕点C顺时针旋转得到图③,若∠CBD=45°,AC=6,BD=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中![]() 如图
如图![]() ,已知抛物线
,已知抛物线![]() ,经过点
,经过点![]() 、
、![]() .
.

![]() 求此抛物线顶点C的坐标;
求此抛物线顶点C的坐标;
![]() 联结AC交y轴于点D,联结BD、BC,过点C作
联结AC交y轴于点D,联结BD、BC,过点C作![]() ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为32个单位长度,点A在原点的左边,距离原点5个单位长度,点B在原点的右边。
(1)点A所对应的数是___,点B对应的数是___;
(2)若已知在数轴上的点E从点A出发向左运动,速度为每秒2个单位长度,同时点F从点B出发向左运动,速度为每秒4个单位长度,在点C处点F追上了点E,求点C对应的数。
(3)若已知在数轴上的点M从点A出发向右运动,速度为每秒2个单位长度,同时点N从点B出发向右运动,速度为每秒4个单位长度,设线段NO的中点为P(O原点),在运动过程中线段POAM的值是否变化?若不变,求其值;若变化,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com