
【题目】阅读下面材料,完成相应的任务:
全等四边形
能够完全重合的两个四边形叫做全等四边形.由此可知,全等四边形的对应边相等、对应角相等;反之,四条边分别相等、四个角也分别相等的两个四边形全等.在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件.根据探究三角形全等条件的经验容易发现,满足1个、2个、3个、4个条件时,两个四边形不一定全等.
在探究“满足5个条件的四边形![]() 和四边形
和四边形![]() 是否全等”时,智慧小组的同学提出如下两个命题:
是否全等”时,智慧小组的同学提出如下两个命题:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 四边形
四边形![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 四边形
四边形![]()
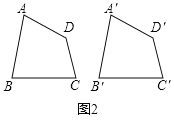
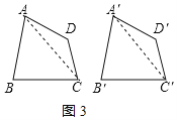
(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是____命题(填“真”或“假”);

(2)小彬经过探究发现命题②是真命题,请你结合图2证明这一命题;
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() ,______,_____,则四边形
,______,_____,则四边形![]() 四边形
四边形![]() ,请在横线上填写两个关于“角”的条件,使该命题为真命题.
,请在横线上填写两个关于“角”的条件,使该命题为真命题.
【答案】(1)假;(2)证明见解析;(3)![]() ,
,![]() .
.
【解析】
(1)观察图1知有对应边不相等,进而求解;
(2)连接![]() ,
,![]() ,证明△ABD≌△A′B′D′,△BCD≌△B′C′D′,根据全等三角形的性质进行求证;
,证明△ABD≌△A′B′D′,△BCD≌△B′C′D′,根据全等三角形的性质进行求证;
(3)连接AC、A′C′,证明△ABC≌△A′B′C′,△ACD≌△A′C′D′,根据全等三角形的性质得出结论.
(1)解:观察图1知,![]() ,
,![]() ,
,![]() ,
,
∴命题①是假命题,
故答案为:假;
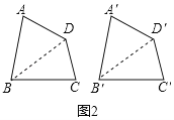
(2)证明:连接![]() ,
,![]() ,如图2所示,
,如图2所示,
在△ABD和△A′B′D′中, ,
,
∴△ABD≌△A′B′D′(SAS),
∴BD=B′D′,∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,
在△BCD和△B′C′D′中,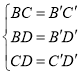 ,
,
∴△BCD≌△B′C′D′(SSS),
∴∠C=∠C′,∠CBD=∠C′B′D′,∠BDC=∠B′D′C′,
∵∠ABC=∠ABD+∠CBD,∠A′B′C′=∠A′B′D′+∠C′B′D′,
∠CDA=∠ADB+∠BDC,∠C′D′A′=∠A′D′B′+∠B′D′C′,
∴∠ABC=∠A′B′C′,∠CDA=∠C′D′A′,
∴四边形ABCD≌四边形![]() ;
;
(3)解:若AB=A′B′,BC=B′C′,CD=C′D',∠B=∠B′,∠C=∠C′,则四边形ABCD≌四边形![]() ;
;
理由如下:
连接AC、A′C′,如图3所示,
在△ABC和△A′B′C′中, ,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠BAC=∠B′A′C′,∠BCA=∠B′C′A′,
∵∠BCD=∠B′C′D′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D′中,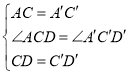 ,
,
∴△ACD≌△A′C′D′(SAS),
∴AD=A′D′,∠D=∠D′,∠CAD=∠C′A′D′,
∵∠BAD=∠BAC+∠CAD,∠B′A′D′=∠B′A′C′+∠C′A′D′,
∴∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形![]() ,
,
故答案为:![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,学校决定围绕“音乐、体育、美术、书法、其它活动项目中,你参加哪一项活动(每人只限一项)的问题”,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题:

(1)在这次调查中一共抽查了多少名学生?
(2)求参加“音乐”活动项目的人数占抽查总人数的百分比.
(3)若全校有2400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步了解![]() ,
,![]() ,
,![]() ,
,![]() 四名老师在学生中受欢迎的程度,学校随机抽取了
四名老师在学生中受欢迎的程度,学校随机抽取了![]() 个学生进行调查(被调查的学生必须选且只能选其中的一名老师),并将调查结果绘制成了如下两幅不完整的统计图:
个学生进行调查(被调查的学生必须选且只能选其中的一名老师),并将调查结果绘制成了如下两幅不完整的统计图:
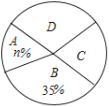
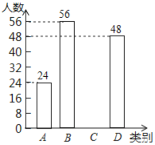
(1)求![]() 和
和![]() 的值;
的值;
(2)扇形统计图中,![]() 对应的圆心角的度数是多少?
对应的圆心角的度数是多少?
(3)求出![]() 的人数,并补全条形统计图.
的人数,并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AB=2,边AB在x轴上,BC边上的中线AD的反向延长线交y轴于点E(0,3),反比例函数y=![]() (x>0)的图象过点C,则k的值为_____.
(x>0)的图象过点C,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
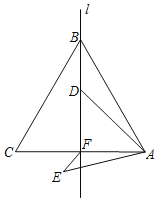
【题目】如图,等边三角形△ABC的边长为6,l是AC边上的高BF所在的直线,点D为直线l上的一动点,连接AD,并将AD绕点A逆时针旋转60°至AE,连接EF,则EF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
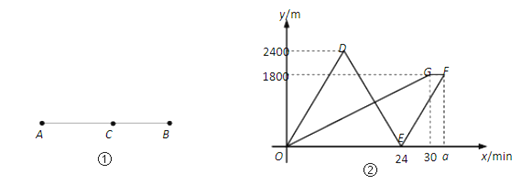
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.
(1)小明的速度为 m/min,图②中a的值为 .
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度,在该校随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多:C.了解较少:D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图.请根据两幅统计图中的信息回答下列问题:
(1)本次被抽取的学生共有_______名;
(2)请补全条形图;
(3)扇形图中的选项“C.了解较少”部分所占扇形的圆心角的大小为_______°;
(4)若该校共有![]() 名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com