
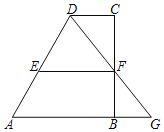
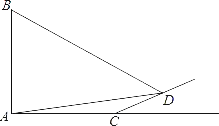
【题目】如图,四边形ABCD中,AB∥CD,CD≠AB,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:CFFG=DFBF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=12,EF=8,求CD的长.
【答案】(1)证明见解析;(2)4.
【解析】
(1)证明△CDF∽△BGF可得出结论;
(2)证明△CDF≌△BGF,可得出DF=GF,CD=BG,得出EF是△DAG的中位线,则2EF=AG=AB+BG,求出BG即可.
(1)证明:∵四边形ABCD,AB∥CD,
∴∠CDF=∠G,∠DCF=∠GBF,
∴△CDF∽△BGF.
∴![]() ,
,
∴CFFG=DFBF;
(2)解:由(1)△CDF∽△BGF,
又∵F是BC的中点,BF=FC,
∴△CDF≌△BGF(AAS),
∴DF=GF,CD=BG,
∵AB∥DC∥EF,F为BC中点,
∴E为AD中点,
∴EF是△DAG的中位线,
∴2EF=AG=AB+BG.
∴BG=2EF﹣AB=2×8﹣12=4,
∴BG=4.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
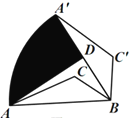
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
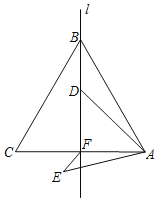
【题目】如图,等边三角形△ABC的边长为6,l是AC边上的高BF所在的直线,点D为直线l上的一动点,连接AD,并将AD绕点A逆时针旋转60°至AE,连接EF,则EF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三位数,它的各个数位上的数字都不为零,且满足百位上的数字与个位上的数字的平均数等于十位上的数字,则称这个三位数为开合数.设![]() 为一个开合数,将
为一个开合数,将![]() 的百位数字与个位数字交换位置后得到的新数再与
的百位数字与个位数字交换位置后得到的新数再与![]() 相加的和记为
相加的和记为![]() .例如:852是“开合数”,则
.例如:852是“开合数”,则![]() .
.
(1)已知开合数![]() (
(![]() ,且为
,且为![]() 整数),求
整数),求![]() 的值;
的值;
(2)三位数![]() 是一个开合数,若百位数字小于个位数字,
是一个开合数,若百位数字小于个位数字,![]() 是一个整数,且
是一个整数,且![]() 能被个位数字与百位数字的差整除,请求满足条件的所有
能被个位数字与百位数字的差整除,请求满足条件的所有![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
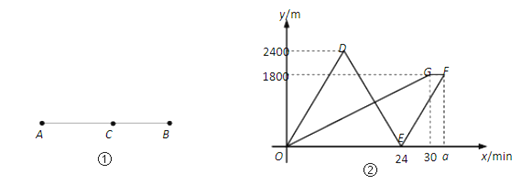
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.
(1)小明的速度为 m/min,图②中a的值为 .
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根![]() 型跳绳和1根
型跳绳和1根![]() 型跳绳共需56元,1根
型跳绳共需56元,1根![]() 型跳绳和2根
型跳绳和2根![]() 型跳绳共需82元.
型跳绳共需82元.
(1)求一根![]() 型跳绳和一根
型跳绳和一根![]() 型跳绳的售价各是多少元?
型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且![]() 型跳绳的数量不多于
型跳绳的数量不多于![]() 型跳绳数量的3倍,请设计出最省钱的购买方案,并说明理由.
型跳绳数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块直角三角板如图1放置,等腰直角三角板![]() 的直角顶点是点
的直角顶点是点![]() ,
,![]() ,直角板
,直角板![]() 的直角顶点
的直角顶点![]() 在
在![]() 上,且
上,且![]() ,
,![]() .三角板
.三角板![]() 固定不动,将三角板
固定不动,将三角板![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]()
![]() .
.
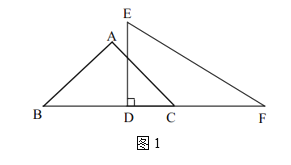
(1)当![]() _______时,
_______时,![]() ;
;
(2)当![]() 时,三角板
时,三角板![]() 绕点
绕点![]() 逆时针旋转至如图2位置,设
逆时针旋转至如图2位置,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
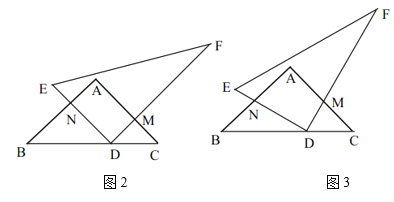
(3)如图3,设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的表达式(不用写
的表达式(不用写![]() 的取值范围).
的取值范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com