
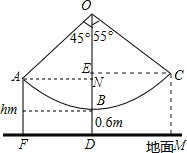
����Ŀ��ij��ũ����������һ����ǧ��������ͼ��ʾ����ǧ����OB�ij�Ϊ3m����ֹʱ��̤�嵽�������BD�ij�Ϊ0.6m��̤���Ⱥ��Բ��ƣ���Ϊ��ȫ��������������涨����ͯ������ȫ�߶���Ϊhm�����˵�����ȫ�߶���Ϊ2m����������ȷ��0.1m��
��1��������OA��OB��45���н�ʱ��ǡΪ��ͯ�İ�ȫ�߶ȣ���h���� ��m
��2��ij����������ǧʱ������OC��OB�����н�Ϊ55�����ʴ����Ƿ�ȫ�����ο����ݣ�![]() ��1.41��sin55���0.82��cos55���0.57��tan55���1.43��
��1.41��sin55���0.82��cos55���0.57��tan55���1.43��

���𰸡���1��1.5����2�������ǰ�ȫ�ģ�
��������
��1���������Ҷ��������OE���ٸ���AF=OB+BD�����DE�����ɵó�h��ֵ��
��2����C����CM��DF����DF�ڵ�M��������֪���������Ҷ������OE���ٸ���CM=OB+DE-OE�����CM��������˵�����ȫ�߶������бȽϣ����ɵó��𰸣�
�⣺��1����Rt��ANO�У���ANO��90����
��cos��AON��![]() ��
��
��ON��OAcos��AON��
��OA��OB��3m����AON��45����
��ON��3cos45���2.12m��
��ND��3+0.6��2.12��1.5m��
��h��ND��AF��1.5m��
�ʴ�Ϊ1.5��
��2����ͼ����C����CM��DF����DF�ڵ�M��
��Rt��CEO����CEO��90����
��cos��COE��![]() ��
��
��OE��OCcos��COF��
��OB��OC��3m����CON��55����
��OE��3cos55���1.72m��
��ED��3+0.6��1.72��1.9m��
��CM��ED��1.9m��
�߳��˵�����ȫ�߶���Ϊ2m��
������ǰ�ȫ�ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
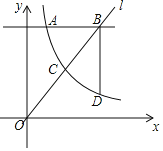
����Ŀ����ͼ������������y��![]() ��x��0����ͼ����ֱ��y��mx���ڵ�C��ֱ��l��y��4�ֱ�������ͼ���ڵ�A��1��4���͵�B������B��BD��l������������ͼ���ڵ� D��
��x��0����ͼ����ֱ��y��mx���ڵ�C��ֱ��l��y��4�ֱ�������ͼ���ڵ�A��1��4���͵�B������B��BD��l������������ͼ���ڵ� D��
��1�����������Ľ���ʽ��
��2����BD��2ABʱ�����B�����ꣻ
��3���ڣ�2���������£�ֱ��д������ʽ![]() ��mx�Ľ⼯��
��mx�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
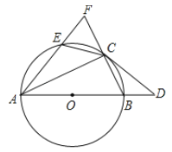
����Ŀ����ͼ��EΪԲO�ϵ�һ�㣬CΪ�ӻ�EB���е㣮CD��![]() �ڵ�C����
�ڵ�C����![]() ��ֱ��AB���ӳ����ڵ�D���ӳ��߶�AE���߶�BC��ʹ֮���ڵ�F��
��ֱ��AB���ӳ����ڵ�D���ӳ��߶�AE���߶�BC��ʹ֮���ڵ�F��
��1����֤��![]() ��
��![]() ���ǵ��������Σ�
���ǵ��������Σ�
��3����![]() ��
��![]() ����EF�ij���
����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ԥ��ij�����з�չǰ;����1600Ԫ����һ�����ϣ����к��Ȼ����Ӧ������6000Ԫ�����������ϣ��ڶ������ϵ������ǵ�һ����3���������۱ȵ�һ����2Ԫ.
(1)��һ�����Ͻ������۶���Ԫ��
(2)�����ι������ϰ�ͬһ�۸����ۣ�����ȫ���������������1200Ԫ����ô���۵�������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��AC���ϵ��е㣬����BD���ѡ�BDC����BD���ۣ��õ���![]() ��DC��AB���ڵ�E������
��DC��AB���ڵ�E������![]() ����AD=AC��=2��BD=3���D��BC�ľ���Ϊ�� ��
����AD=AC��=2��BD=3���D��BC�ľ���Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��5�£������������Ի���ᡱ�ڱ����ɹ��ٰ죬ij�о�����Ϊ���˽�10-60�������������Ա��δ��Ĺ�ע�̶ȣ����ѡȡ��100�������ڸ÷�Χ�ڵ���������˵��飬�����Ѽ����������Ƴ����в�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��������ʾ��
��� | ����� | Ƶ���������� |
��һ�� |
| 5 |
�ڶ��� |
|
|
������ |
| 35 |
������ |
| 20 |
������ |
| 15 |
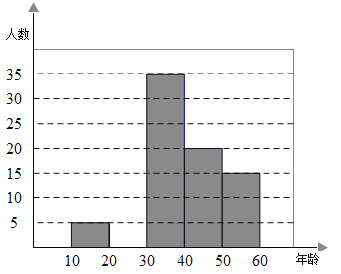

��ֱ��д����3������������ͳ��ͼ������Ӧ��Բ�Ľ���_________�ȣ������������10-60�������300���ˣ���40-50������εĹ�ע���δ�������Լ��___________���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�![]() ��
��![]() ��AB��CD֮��ľ�����8������P���߶�AB�ϴӵ�A������AB������ÿ��2����λ���ٶ������˶�������Q���߶�BC�ϴӵ�B������BC�ķ�����ÿ��1����λ���ٶ������˶�������P��
��AB��CD֮��ľ�����8������P���߶�AB�ϴӵ�A������AB������ÿ��2����λ���ٶ������˶�������Q���߶�BC�ϴӵ�B������BC�ķ�����ÿ��1����λ���ٶ������˶�������P��![]() �����߶�AD�ڵ�E����
�����߶�AD�ڵ�E����![]() ����ͬʱ���������˶�ʱ��Ϊ
����ͬʱ���������˶�ʱ��Ϊ![]() �룬
�룬![]() ��
��
��1����![]() Ϊ��ֵʱ��BEƽ��
Ϊ��ֵʱ��BEƽ��![]() ��
��
��2������PQ,CE�����ı���PECQ�����ΪS�����S��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() �������ڣ���ֱ�Ӹ�����ʱ
�������ڣ���ֱ�Ӹ�����ʱ![]() ��ֵ������д˵�����̣����������ڣ���˵�����ɣ�
��ֵ������д˵�����̣����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ͼ����Ǹ������ҵ�����ijɱ�ѹ����ij�е�������˼ۣ��������������б���ͼ������![]() ��
��![]() ��
��![]() ��������
��������
��ʻ·�� | �շѱ� | |
����ǰ | ���ۺ� | |
������ | ��9Ԫ | �� |
���� | ÿ����2Ԫ | ÿ���� |
���� | ÿ���� | |
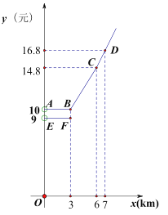
����ʻ·��Ϊ![]() ʱ������ǰ���˼�Ϊ
ʱ������ǰ���˼�Ϊ![]() ��Ԫ�������ۺ���˼�Ϊ
��Ԫ�������ۺ���˼�Ϊ![]() ��Ԫ������ͼ������
��Ԫ������ͼ������![]() ��ʾ
��ʾ![]() ��
��![]() ֮��ĺ�����ϵ���߶�
֮��ĺ�����ϵ���߶�![]() ��ʾ
��ʾ![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵ������ͼ����Ϣ��������и��⣺
֮��ĺ�����ϵ������ͼ����Ϣ��������и��⣺
��1����գ�![]() _____��
_____��![]() _____��
_____��![]() _______��
_______��
��2��д����![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽ��������ͼ�л����ú���ͼ��
֮��ĺ�����ϵʽ��������ͼ�л����ú���ͼ��
��3������ʻ·��Ϊ![]() ʱ�����۵���ǰ���˼۵ĸߵͣ�
ʱ�����۵���ǰ���˼۵ĸߵͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͺŵ�ң��ʽ��þ�Ͻ��¥��������ͼ��ʾ������ң�ذ�ť���������Զ����£�������䵽¥�����![]() ��ʱ������������ļн�
��ʱ������������ļн�![]() �����ǵ�����¥��ʱ��ȫ�����ʵȷ������أ��뽫�����������ļнǵ�����
�����ǵ�����¥��ʱ��ȫ�����ʵȷ������أ��뽫�����������ļнǵ�����![]() ���ֲ��
���ֲ��![]() �����������
�����������![]() ��
��![]() ��ľ���Ϊ
��ľ���Ϊ![]() �����ӵĿ���
�����ӵĿ���![]() ��
��
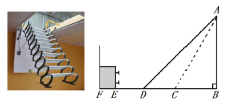
��1����¥���![]() ��¥�����ĸ߶�
��¥�����ĸ߶�![]() ��
��
��2�������ݰ�װ���ˮƽ����![]() ������ȷ��
������ȷ��![]() ���ο����ݣ�
���ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com