
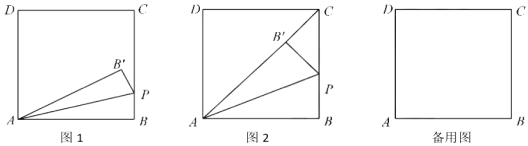
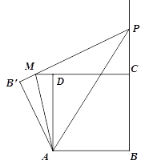
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
【答案】(1)①![]() ;②t=2或t=6或t=2
;②t=2或t=6或t=2![]() (2)见解析.
(2)见解析.
【解析】
(1)①先利用勾股定理求出AC长,再根据△APB≌△APB′,继而根据全等三角形的性质推导得出∠B=∠PB′C=90°,B′C= ![]() ,再证明
,再证明![]() ,根据相似三角形的性质求出PB′=2
,根据相似三角形的性质求出PB′=2![]() -4,由此即可求得答案;
-4,由此即可求得答案;
②根据题意分三种情况,分别画出图形,结合图形分别讨论求解即可;
(2)如图,根据∠PAM=45°以及翻折的性质可以证明得到△DAM≌△B′AM,从而可得AD=AB′=AB,证得四边形ABCD是正方形,继而根据题意画出图形,根据翻折的性质以及全等三角形的知识进行推导即可求得答案.
(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∴AC=![]() ,
,
∵△APB≌△APB′,
∴∠AB′P=∠B=90°,AB′=AB=2![]() ,BP=B′P,
,BP=B′P,
∴∠B=∠PB′C=90°,B′C=AC-AB′=![]() ,
,
又∵∠PCB′=∠ACB,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴PB′=2![]() -4,
-4,
∴PB=2![]() -4,
-4,
即t=2![]() -4;
-4;
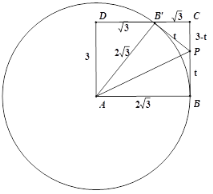
②如图,当∠PCB′=90 °时,此时点B′落在BC上,
在Rt△AB′D中,∠D=90°,∴B′D=![]() ,
,
∴B′C=![]() ,
,
在△PCB′中,由勾股定理得:![]() ,
,
解得t=2;
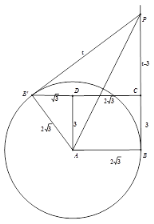
如图,当∠PCB′=90 °时,此时点B′在CD的延长线上,
在Rt△AB′D中,∠ADB′=90°,∴B′D=![]() ,
,
∴B′C=3![]() ,
,
在△PCB′中,由勾股定理得:![]() ,解得t=6;
,解得t=6;
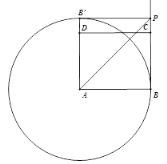
当∠CPB′=90 °时,易得四边形ABPB′为正方形,
∴BP=AB=2![]() ,
,
解得t=2![]() ;
;
综上,t=2或t=6或t=2![]() ;
;
(2)如图

∵∠PAM=45°,
∴∠2+∠3=45°,∠1+∠4=45°,
又∵翻折,
∴∠1=∠2,∠3=∠4,
又∵∠ADM=∠AB′M=90°,AM=AM,
∴△DAM≌△B′AM,
∴AD=AB′=AB,
∴四边形ABCD是正方形,
如图,
设∠APB=x,
∴∠PAB=90°-x,
∴∠DAP=x,
∵AD=AB′,AM=AM,∠ADM=∠AB′M=90°,
∴Rt△MDA≌Rt△B′AM(HL),
∴∠B′AM=∠DAM,
∵翻折,
∴∠PAB=∠PAB′=90°-x,
∴∠DAB′=∠PAB′-∠DAP=90°-2x,
∴∠DAM=![]() ∠DAB′=45°-x,
∠DAB′=45°-x,
∴∠MAP=∠DAM+∠PAD=45°.


科目:初中数学 来源: 题型:
【题目】吸烟有害健康,为配合“戒烟”运动,有所初中学校组织同学们到社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅统计图(待完善).根据统计图解答下列问题:
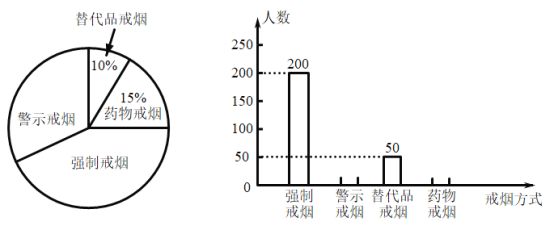
(1)将条形统计图补充完整.
(2)若这个社区约有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(3)为了让更多市民增强“戒烟”意识,同学们在社区作了两期“警示戒烟”宣传.在(2)的条件下,若每期宣传后,市民支持“警示戒烟”平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
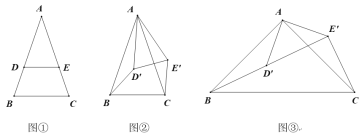
如图①,在△ABC中,AB=AC,点D、E分别为线段AB、AC上的点,且DE∥BC.将△ADE绕点A旋转一定的角度后得到△AD′E′,如图②.
(1)求证:△ABD′≌△ACE′.
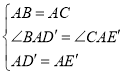
(深入研究)
如图③,![]() ,
,![]() ,
,![]() .
.
(2)若点D′在线段BE′上,求△BCE′的面积.
(3)若点B、D′、E′不在同一直线上,且点![]() 在
在![]() 内,顺次连结C、B、D′、E′四点,则四边形CBD′E′的面积是否改变,若改变,请求出改变后的面积;若不变,请说明理由.
内,顺次连结C、B、D′、E′四点,则四边形CBD′E′的面积是否改变,若改变,请求出改变后的面积;若不变,请说明理由.
(拓展延伸)
(4)如图④,在四边形ABCD中,AB∥CD,∠D=∠C≠90°.请用没有刻度的直尺和圆规画出满足下列条件的四边形A′B′CD.
条件1:利用一次旋转变换改变线段AB的位置,得到对应线段A′B′.
条件2:连结A′D、B′C,使得四边形A′B′CD的面积与四边形ABCD的面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A、B、C、D四种不同口味的牛奶供学生饮用,学校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如图所示的两幅不完整的统计图,根据统计图的信息解决下列问题:
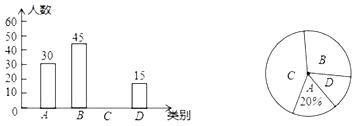
(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的圆心角度数是 ;
(4)若该校有400名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A、B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
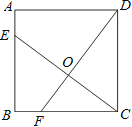
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣
x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣![]() x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.
x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.
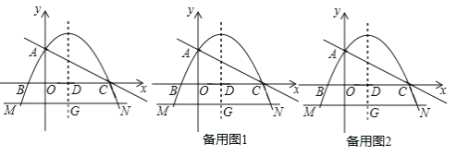
(1)求此抛物线的解析式.
(2)求点N的坐标.
(3)过点A的直线与抛物线交于点F,当tan∠FAC=![]() 时,求点F的坐标.
时,求点F的坐标.
(4)过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤![]() ),请直接写出S与t的函数关系式.
),请直接写出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
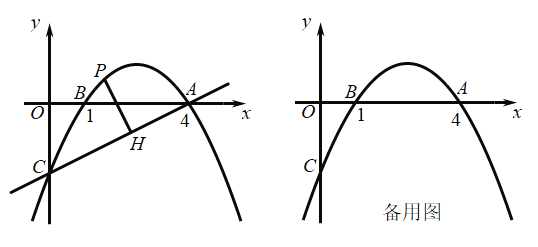
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com