
【题目】某品牌牛奶供应商提供A、B、C、D四种不同口味的牛奶供学生饮用,学校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如图所示的两幅不完整的统计图,根据统计图的信息解决下列问题:
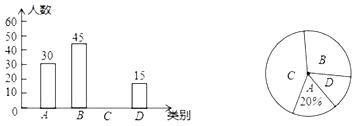
(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的圆心角度数是 ;
(4)若该校有400名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A、B口味的牛奶共约多少盒?
【答案】(1)150人;(2)见解析;(3)144°;(4)200盒
【解析】
(1)利用A类别人数及其百分比可得总人数;
(2)总人数减去A、B、D类别人数,求得C的人数,即可补全统计图;
(3)用360°乘以C类别人数所占比即可得出答案;
(4)总人数乘以样本中A、B人数占总人数的比例即可.
解:(1)本次调查的学生有:30÷20%=150(人);
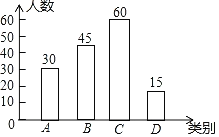
(2)C类别人数为:150-(30+45+15)=60(人),补全条形图如下:
(3)扇形统计图中C对应的圆心角度数是360°×![]() =144°
=144°
故答案为:144°.
(4)根据题意得:400×![]() =200(人),
=200(人),
答:该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约200盒.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)求证:AC是⊙O的切线;
(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;
(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).
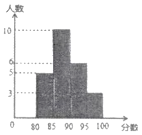
(1)分数段在______范围的人数最多;
(2)全校共有________人参加比赛;
(3)学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示在矩形ABCD中,AB=6,AD=3,点E、F分别是边DC、DA的三等分点(DE![]() EC,DF
EC,DF![]() AF),四边形DFGE为矩形,连接BG.
AF),四边形DFGE为矩形,连接BG.
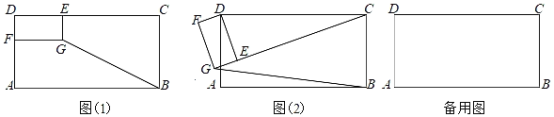
(1)问题发现:在图(1)中,![]() = ;
= ;
(2)拓展探究:将图(1)中的矩形DFGE绕点D旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图(2)的情形给出证明;
的大小有无变化?请仅就图(2)的情形给出证明;
(3)问题解决:当矩形DFGE旋转至B、G、E三点共线时,请直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
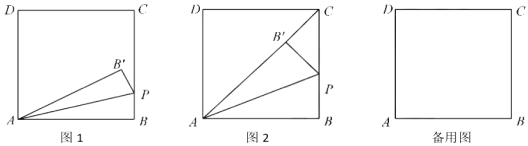
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
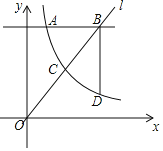
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
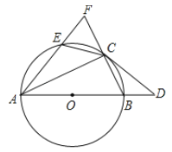
【题目】如图,E为圆O上的一点,C为劣弧EB的中点.CD切![]() 于点C,交
于点C,交![]() 的直径AB的延长线于点D.延长线段AE和线段BC,使之交于点F.
的直径AB的延长线于点D.延长线段AE和线段BC,使之交于点F.
(1)求证:![]() 和
和![]() 都是等腰三角形;
都是等腰三角形;
(3)若![]() ,
,![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com