
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x2+bx+c��x�ύ��B��C���㣬��y�ύ�ڵ�A��ֱ��y����
x2+bx+c��x�ύ��B��C���㣬��y�ύ�ڵ�A��ֱ��y����![]() x+2����A��C���㣬�����ߵĶԳ�����x�ύ�ڵ�D��ֱ��MN��Գ��ύ�ڵ�G���������߽���M��N���㣨��N�ڶԳ����Ҳࣩ����MN��x�ᣬMN��7��
x+2����A��C���㣬�����ߵĶԳ�����x�ύ�ڵ�D��ֱ��MN��Գ��ύ�ڵ�G���������߽���M��N���㣨��N�ڶԳ����Ҳࣩ����MN��x�ᣬMN��7��
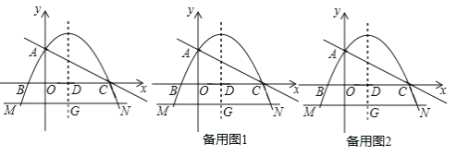
��1����������ߵĽ���ʽ��
��2�����N�����꣮
��3������A��ֱ���������߽��ڵ�F����tan��FAC��![]() ʱ�����F�����꣮
ʱ�����F�����꣮
��4������D��ֱ��AC�Ĵ��ߣ���AC�ڵ�H����y���ڵ�K������CN����AHK������AC��ÿ��1����λ���ȵ��ٶ��ƶ����ƶ������С�AHK���ı���DGNC�����ص������ص����ΪS���ƶ�ʱ��Ϊt��0��t��![]() ������ֱ��д��S��t�ĺ�����ϵʽ��
������ֱ��д��S��t�ĺ�����ϵʽ��
���𰸡���1��y����![]() x2+
x2+![]() x+2����2����N��������5��-3������3����F����������3��2����
x+2����2����N��������5��-3������3����F����������3��2����![]() ����
����![]() ������4��
������4��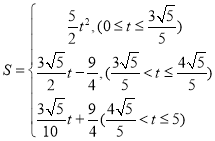 ��
��
��������
��1����A��C������ֱ�Ϊ��0��2������4��0��������A��C������������߱���ʽ������⣻
��2�������ߵĶԳ���Ϊ��x��![]() ����N�ĺ�����Ϊ��
����N�ĺ�����Ϊ��![]() ��������⣻
��������⣻
��3���ֵ�F��ֱ��AC�·�����F��ֱ��AC���Ϸ�����������ֱ���⼴�ɣ�
��4����0��t��![]() ����
����![]() ��t��
��t��![]() ��
��![]() ��t��
��t��![]() ����������ֱ���⼴�ɣ�
����������ֱ���⼴�ɣ�
�⣺��1��ֱ��y����![]() x+2����A��C���㣬���A��C������ֱ�Ϊ��0��2������4��0����
x+2����A��C���㣬���A��C������ֱ�Ϊ��0��2������4��0����
��c��2�������߱���ʽΪ��y����![]() x2+bx+2��
x2+bx+2��
����C���������ʽ����ã�b��![]() ��
��
�������ߵı���ʽΪ��y����![]() x2+
x2+![]() x+2���٣�
x+2���٣�
��2�������ߵĶԳ���Ϊ��x��![]() ��
��
��N�ĺ�����Ϊ�� ![]() ��
��
�ʵ�N������Ϊ��5��-3����
��3����tan��ACO��![]() ��tan��FAC��
��tan��FAC��![]() ��
��
����ACO����FAC��
�ٵ���F��ֱ��AC�·�ʱ��
��ֱ��AF��x���ڵ�R��

�ߡ�ACO����FAC����AR��CR��
���R��r��0������r2+4����r��4��2����ã�r��![]() ��
��
����R����������![]() ��0����
��0����
����R��A���������һ�κ�������ʽ��y��mx+n�ã� ��
��
��ã� ��
��
��ֱ��AR�ı���ʽΪ��y����![]() x+2���ڣ�
x+2���ڣ�
�����٢ڲ���ã�x��![]() ���ʵ�F��
���ʵ�F��![]() ����
����![]() ����
����
�ڵ���F��ֱ��AC���Ϸ�ʱ��
�ߡ�ACO����F��AC����AF���x�ᣬ
���F�䣨3��2����
���ϣ���F������Ϊ����3��2����![]() ����
����![]() ����
����
��4����ͼ2�����ACO��������tan����![]() ����sin����
����sin����![]() ��cos����
��cos����![]() ��
��
�ٵ�0��t��![]() ʱ�����ͼ����
ʱ�����ͼ����
���AHK�ƶ�����A��H��K���λ��ʱ��ֱ��H��K��ֱ�x���ڵ�T���������߶Գ����ڵ�S��

���DST����ACO����������T��TL��KH��
��LT��HH�䣽t����LTD����ACO������
��DT�� ��DS��
��DS��![]() ��
��
S��S��DST��![]() DT��DS��
DT��DS��![]() ��
��
�ڵ�![]() ��t��
��t��![]() ʱ���Ҳ�ͼ����
ʱ���Ҳ�ͼ����
ͬ���ɵã�
S��![]() ��
��![]() DG����GS��+DT�䣩��
DG����GS��+DT�䣩��![]() 3+��
3+��![]() +
+![]() ��
��![]() ����
����![]() ��
��
�۵�![]() ��t��
��t��![]() ʱ��ͬ���ɵ�S=
ʱ��ͬ���ɵ�S=![]() ��
��
���ϣ�S�� ��
��


 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������������Ϣ��
��ab��0����a+b+c��0����b+2c��0����a��2b+4c��0����![]() ��
��
����Ϊ������ȷ��Ϣ�ĸ�����

A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ǵȱ�������
�ǵȱ�������![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��
��![]() ������
������![]() ���ŵ�
���ŵ�![]() ��ʱ����ת��õ�
��ʱ����ת��õ�![]() ����
����![]() �Ķ�����_______��
�Ķ�����_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
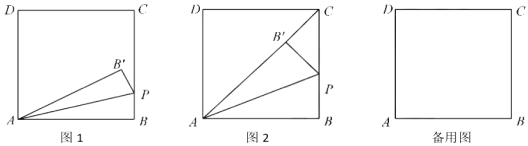
����Ŀ����ͼ1���ھ���![]() �У�BC=3������
��BC=3������![]() ��
��![]() ��������ÿ��1����λ���ٶȣ�������
��������ÿ��1����λ���ٶȣ�������![]() �����ƶ�����
�����ƶ�����![]() ����ֱ��
����ֱ��![]() �ĶԳ�
�ĶԳ�![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]()
��1����![]()
����ͼ2������B������AC��ʱ����Ȼ��PCB����ֱ�������Σ����ʱt��ֵ
���Ƿ��������ͼ2��ʱ�̣�ʹ����PCB����ֱ�������Σ������ڣ���ֱ��д�����з��������t��ֵ���������ڣ���˵������
��2����P�㲻��C���غ�ʱ����ֱ��PB����ֱ��CD�ཻ�ڵ�M���ҵ�t��3ʱ����ijһʱ���н��ۡ�PAM=45����������̽��������t��3������ʱ�̣����ۡ�PAM=45���Ƿ����dz�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC=80�㣬��BAC=40��.
��1���߹���ͼ����AB�Ĵ�ֱƽ����DE���ֱ���AC��AB���ڵ�D��E��������BD����������ͼ�ۼ�����д������

��2��֤������ABC�ס�BDC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
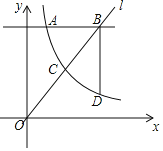
����Ŀ����ͼ������������y��![]() ��x��0����ͼ����ֱ��y��mx���ڵ�C��ֱ��l��y��4�ֱ�������ͼ���ڵ�A��1��4���͵�B������B��BD��l������������ͼ���ڵ� D��
��x��0����ͼ����ֱ��y��mx���ڵ�C��ֱ��l��y��4�ֱ�������ͼ���ڵ�A��1��4���͵�B������B��BD��l������������ͼ���ڵ� D��
��1�����������Ľ���ʽ��
��2����BD��2ABʱ�����B�����ꣻ
��3���ڣ�2���������£�ֱ��д������ʽ![]() ��mx�Ľ⼯��
��mx�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽���꼶��600��ѧ��ÿ�������ѧϰ������������˾��꼶�IJ���ѧ��������������ÿ������ѧϰ��ʱ�䣮���ݵ�������������������������ͳ��ͼ��ͼ1ͼ2���������ͳ��ͼ�е���Ϣ�ش��������⣺
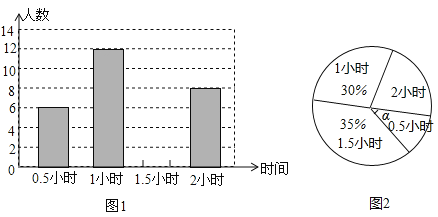
��1�����ε����ѧ�������� �ˣ�
��2��ͼ2�н�![]() �� �ȣ�
�� �ȣ�
��3����ͼ1����ͳ��ͼ����������
��4�������У���꼶ѧ������ѧϰ������1.5Сʱ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���¼�˼ס��ҡ�����������ͬѧ���������ѧ���Գɼ���ƽ�����뷽����ݱ������ݣ�Ҫ����ѡ��һ���ɼ����ҷ����ȶ���ͬѧ�μ���ѧ������Ӧ��ѡ��__________������������ �������� �������� ����������
�� | �� | �� | �� | |
ƽ�������֣� | 92 | 95 | 95 | 92 |
���� | 3.6 | 3.6 | 7.4 | 8.1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��AC���ϵ��е㣬����BD���ѡ�BDC����BD���ۣ��õ���![]() ��DC��AB���ڵ�E������
��DC��AB���ڵ�E������![]() ����AD=AC��=2��BD=3���D��BC�ľ���Ϊ�� ��
����AD=AC��=2��BD=3���D��BC�ľ���Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com