
ЁОЬтФПЁПНёФъжэШтМлИёЪмЗЧжожэЮСвпЧщгАЯьЃЌгаНЯДѓЗљЖШЕФЩЯЩ§ЃЌЮЊСЫНтФГЕиЧјбјжГЛЇЪмЗЧжожэЮСвпЧщИаШОЪмджЧщПіЃЌЯжДгИУЕиЧјНЈЕЕЕФбјжГЛЇжаЫцЛњГщШЁСЫВПЗжбјжГЛЇНјааСЫЕїВщЃЈАбЕїВщНсЙћЗжЮЊЫФИіЕШМЖЃКAМЖЃКЗЧГЃбЯжиЃЛBМЖЃКбЯжиЃЛCМЖЃКвЛАуЃЛDМЖЃКУЛгаИаШОЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭГМЦЭМжаЕФаХЯЂНтОіЯТСаЮЪЬтЃК
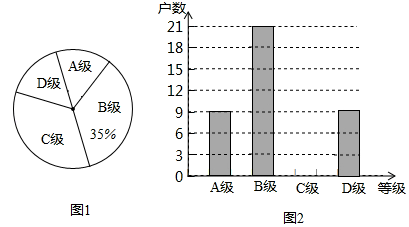
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФбјжГЛЇЕФзмЛЇЪ§ЪЧЁЁ ЁЁЃЛАбЭМ2ЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ2ЃЉШєИУЕиЧјНЈЕЕЕФбјжГЛЇга1500ЛЇЃЌЧѓЗЧГЃбЯжигыбЯжиЕФбјжГЛЇвЛЙВгаЖрЩйЛЇЃП
ЃЈ3ЃЉФГЕїбаЕЅЮЛЯыДг5ЛЇНЈЕЕбјжГЛЇЃЈЗжБ№МЧЮЊaЃЌbЃЌcЃЌdЃЌeЃЉжаЫцЛњбЁШЁСНЛЇЃЌНјвЛВНИњзйМрВтВЁЖОДЋВЅЧщПіЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГібЁжабјжГЛЇeЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ60ЃЛЭММћНтЮіЃЛЃЈ2ЃЉ750ЛЇЃЛЃЈ3ЃЉСаБэМћНтЮіЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉДгСНИіЭГМЦЭМПЩЕУЃЌЁАBМЖЁБЕФга21ЛЇЃЌеМЕїВщзмЛЇЪ§ЕФ35%ЃЌПЩЧѓГіЕїВщзмЛЇЪ§ЃЛЧѓГіЁАCМЖЁБЛЇЪ§ЃЌМДПЩВЙШЋЬѕаЮЭГМЦЭМЃК
ЃЈ2ЃЉбљБОЙРМЦзмЬхЃЌбљБОжаЁАбЯжиЁБКЭЁАЗЧГЃбЯжиЁБеМ![]() ЃЌЙРМЦзмЬх1500ЛЇЕФ
ЃЌЙРМЦзмЬх1500ЛЇЕФ![]() ЪЧЁАбЯжиЁБКЭЁАЗЧГЃбЯжиЁБЕФЛЇЪ§ЃЛ
ЪЧЁАбЯжиЁБКЭЁАЗЧГЃбЯжиЁБЕФЛЇЪ§ЃЛ
ЃЈ3ЃЉгУСаБэЗЈЛђЪїзДЭМЗЈСаОйГіЫљгаЕШПЩФмГіЯжЕФЧщПіЃЌДгжаевГіЗћКЯЬѕМўЕФЧщПіЪ§ЃЌНјЖјЧѓГіИХТЪЃЎ
НтЃКЃЈ1ЃЉ21ЁТ35%ЃН60ЛЇЃЌ60Љ9Љ21Љ9ЃН21ЛЇЃЌ
ЙЪД№АИЮЊЃК60ЃЛ
ВЙШЋЬѕаЮЭГМЦЭМШчЭМЫљЪОЃК

ЃЈ2ЃЉ1500ЁС![]() ЃН750ЛЇЃЌ
ЃН750ЛЇЃЌ
Д№ЃКШєИУЕиЧјНЈЕЕЕФбјжГЛЇга1500ЛЇжаЗЧГЃбЯжигыбЯжиЕФбјжГЛЇвЛЙВга750ЛЇЃЛ
ЃЈ3ЃЉгУБэИёБэЪОЫљгаПЩФмГіЯжЕФЧщПіШчЯТЃК
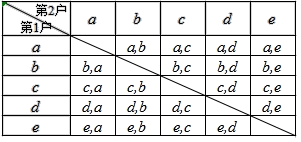
ЙВга20жжВЛЭЌЕФЧщПіЃЌЦфжабЁжаeЕФга8жжЃЌ
ЁрPЃЈбЁжаeЃЉЃН![]() ЃН
ЃН![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
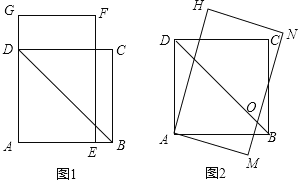
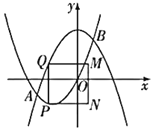
ЁОЬтФПЁПШчЭМ1ЃЌЫФБпаЮABCDЪЧБпГЄЮЊ![]() ЕФе§ЗНаЮЃЌОиаЮAEFGжаAE=4ЃЌЁЯAFE=30ЁуЁЃНЋОиаЮAEFGШЦЕуAЫГЪБеыа§зЊ15ЁуЕУЕНОиаЮAMNHЃЈШчЭМ2ЃЉЃЌДЫЪБBDгыMNЯрНЛгкЕуO.
ЕФе§ЗНаЮЃЌОиаЮAEFGжаAE=4ЃЌЁЯAFE=30ЁуЁЃНЋОиаЮAEFGШЦЕуAЫГЪБеыа§зЊ15ЁуЕУЕНОиаЮAMNHЃЈШчЭМ2ЃЉЃЌДЫЪБBDгыMNЯрНЛгкЕуO.
ЃЈ1ЃЉЧѓЁЯDOMЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЭМ2жаЃЌЧѓDЁЂNСНЕуМфЕФОрРыЃЛ
ЃЈ3ЃЉШєНЋОиаЮAMNHШЦЕуAдйЫГЪБеыа§зЊ15ЁуЕУЕНОиаЮAPQRЃЌДЫЪБЕуBдкОиаЮAPQRЕФФкВПЁЂЭтВПЛЙЪЧБпЩЯЃПВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЗжБ№ЪЧе§ЗНаЮ
ЗжБ№ЪЧе§ЗНаЮ![]() ЕФБп
ЕФБп![]() ЕФжаЕуЃЌвд
ЕФжаЕуЃЌвд![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌСЊНс
ЃЌСЊНс![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЧѓжЄ
ЃЌЧѓжЄ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌЕуEЁЂFЁЂGЁЂHЗжБ№дкABЁЂBCЁЂCDЁЂADБпЩЯЧвAE=CGЃЌAH=CFЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЙћAB=ADЃЌЧвAH=AEЃЌЧѓжЄЃКЫФБпаЮEFGHЪЧОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
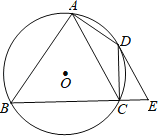
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDФкНггкЁбOЃЌЁЯBAD=90ЁуЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌЧвЁЯDEC=ЁЯBACЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєACЁЮDEЃЌЕБAB=8ЃЌCE=2ЪБЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() КЭХзЮяЯп
КЭХзЮяЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЈЕу
ЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌ
ЕФзѓВрЃЉЃЌ![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЩЯ
ЩЯ![]() ЖЮЕФвЛЕуЃЈЕу
ЖЮЕФвЛЕуЃЈЕу![]() ВЛгы
ВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпНЛХзЮяЯп
жсЕФДЙЯпНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊБпЯђгвВрзїе§ЗНаЮ
ЮЊБпЯђгвВрзїе§ЗНаЮ![]() ЃЎЩшЕу
ЃЎЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЕБе§ЗНаЮЕФЫФИіЖЅЕуЗжБ№ТфдкЫФИіВЛЭЌЯѓЯоЪБЃЌ
ЃЌЕБе§ЗНаЮЕФЫФИіЖЅЕуЗжБ№ТфдкЫФИіВЛЭЌЯѓЯоЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§yЃНЉ![]() x+2ЕФЭМЯѓЃЌШЦxжсЩЯвЛЕуPЃЈmЃЌ0ЃЉа§зЊ180ЁуЃЌЫљЕУЕФЭМЯѓОЙ§ЃЈ0ЃЎЉ1ЃЉЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ
x+2ЕФЭМЯѓЃЌШЦxжсЩЯвЛЕуPЃЈmЃЌ0ЃЉа§зЊ180ЁуЃЌЫљЕУЕФЭМЯѓОЙ§ЃЈ0ЃЎЉ1ЃЉЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.Љ2B.Љ1C.1D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(12Зж)ШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃН8ЃЌBCЃН6ЃЌCDЁЭABгкЕуD.ЕуPДгЕуDГіЗЂЃЌбиЯпЖЮDCЯђЕуCдЫЖЏЃЌЕуQДгЕуCГіЗЂЃЌбиЯпЖЮCAЯђЕуAдЫЖЏЃЌСНЕуЭЌЪБГіЗЂЃЌЫйЖШЖМЮЊУПУы1ИіЕЅЮЛГЄЖШЃЌЕБЕуPдЫЖЏЕНCЪБЃЌСНЕуЖМЭЃжЙЃЎЩшдЫЖЏЪБМфЮЊtУыЃЎ
(1)ЧѓЯпЖЮCDЕФГЄЃЛ
(2)ЩшЁїCPQЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂШЗЖЈдкдЫЖЏЙ§ГЬжаЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУSЁїCPQЁУSЁїABCЃН9ЁУ100ЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
(3)ЕБtЮЊКЮжЕЪБЃЌЁїCPQЮЊЕШбќШ§НЧаЮЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
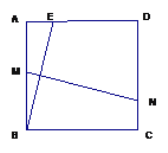
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌAB=![]() ЃЌEЪЧADБпЩЯЕФвЛЕу(ЕуEгыЕуAКЭЕуDВЛжиКЯ)ЃЌBEЕФДЙжБЦНЗжЯпНЛABгкЕуMЃЌНЛDCгкЕуN.
ЃЌEЪЧADБпЩЯЕФвЛЕу(ЕуEгыЕуAКЭЕуDВЛжиКЯ)ЃЌBEЕФДЙжБЦНЗжЯпНЛABгкЕуMЃЌНЛDCгкЕуN.
(1)жЄУїЃКMN = BE.
(2)ЩшAE=![]() ЃЌЫФБпаЮADNMЕФУцЛ§ЮЊSЃЌаДГіSЙигк
ЃЌЫФБпаЮADNMЕФУцЛ§ЮЊSЃЌаДГіSЙигк![]() ЕФКЏЪ§ЙиЯЕЪН.
ЕФКЏЪ§ЙиЯЕЪН.
(3)ЕБAEЮЊКЮжЕЪБЃЌЫФБпаЮADNMЕФУцЛ§зюДѓЃПзюДѓжЕЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com