
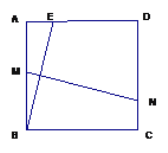
【题目】如图,在正方形ABCD中,AB=![]() ,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
(1)证明:MN = BE.
(2)设AE=![]() ,四边形ADNM的面积为S,写出S关于
,四边形ADNM的面积为S,写出S关于![]() 的函数关系式.
的函数关系式.
(3)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
【答案】(1)证明见解析;(2)S=-![]() x2+x+2;(3)当AE =1时,四边形ADNM的面积S的值最大,最大值是
x2+x+2;(3)当AE =1时,四边形ADNM的面积S的值最大,最大值是![]() .
.
【解析】
(1)作辅助线ME、MN,由SAS证明△EBA≌△MNF,从而得证;
(2)连接ME,构造出直角三角形△AME,在Rt△AME中,AE=x,ME=MB=2-AM,可得(2-AM)2=x2+AM2,解得AM,由(1)△EBA≌△MNF,可得EA=MF,由此DN=AF=AM+MF=AM+AE,即可求得四边形ADNM的面积为-![]() x2+x+2;
x2+x+2;
(3)根据(2)的答案,利用二次函数的最值问题即可求出.
(1)设MN交BE于P,根据题意,得MN⊥BE,
过N作AB的垂线交AB于F,

在Rt△AEB和Rt△MNF中,
∠MBP+∠BMN=90°,∠FNM+∠BMN=90°,
∴∠MBP=∠MNF,
又AB=FN,
∴Rt△EBA≌Rt△MNF,故MN=BE;
(2)连接ME,
根据题意,得MB=ME,
在Rt△AME中,AE=x,ME=MB=2-AM,
∴(2-AM)2=x2+AM2,
解得AM=1-![]() x2,
x2,
由(1)△EBA≌△MNF,
∴EA=MF,
∴DN=AF=AM+MF=AM+AE,
∴四边形ADNM的面积S=![]() ×AD=
×AD=![]() ×2=2AM+AE=2(1-
×2=2AM+AE=2(1-![]() x2)+x=-
x2)+x=-![]() x2+x+2,
x2+x+2,
即所求关系式为S=-![]() x2+x+2;
x2+x+2;
(3)s=-![]() x2+x+2=-
x2+x+2=-![]() (x2-2x+1)+
(x2-2x+1)+![]() =-
=-![]() (x-1)2+
(x-1)2+![]() ,
,
故当AE=x=1时,四边形ADNM的面积S的值最大,最大值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
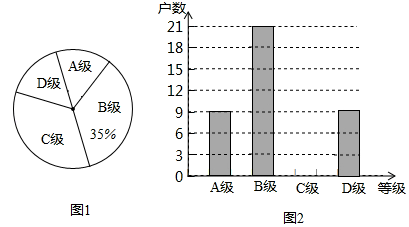
(1)本次抽样调查的养殖户的总户数是 ;把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?
(3)某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,1),B(1,0),PQ是直线y=x上的一条动线段且PQ=![]() (Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.
(Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“加倍”矩形.
的“加倍”矩形.
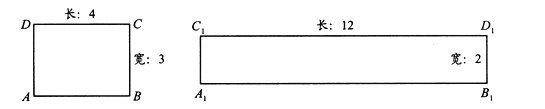
解决问题:
(1)当矩形的长和宽分别为3,2时,它是否存在“加倍”矩形?若存在,求出“加倍”矩形的长与宽,若不存在,请说明理由.
(2)边长为![]() 的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
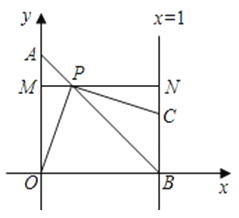
【题目】如图,以 ![]() 为原点的直角坐标系中,
为原点的直角坐标系中, ![]() 点的坐标为(0, 1),直线
点的坐标为(0, 1),直线 ![]() 交
交![]() 轴于点
轴于点![]() .
.![]() 为线段
为线段![]() 上一动点,作直线
上一动点,作直线![]() ,交直线
,交直线![]() 于点
于点![]() . 过
. 过![]() 点作直线
点作直线![]() 平行于
平行于![]() 轴,交
轴,交![]() 轴于点
轴于点 ![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当点![]() 在第一象限时,求证:
在第一象限时,求证:![]() ;
;
(2)当点![]() 在第一象限时,设
在第一象限时,设![]() 长为
长为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与![]() 间的函数关系式,并写出自变量
间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 也随之在直线
也随之在直线![]() 上移动,
上移动,![]() 是否可能成为等腰三角形?如果可能,求出所有能使
是否可能成为等腰三角形?如果可能,求出所有能使![]() 成为等腰直角三角形的点
成为等腰直角三角形的点![]() 的坐标;如果不可能,请说明理由.
的坐标;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率的试验时,统计了某一结果出现的频率,绘制了如图所示折线统计图,则符合这一结果的试验最有可能的是( )
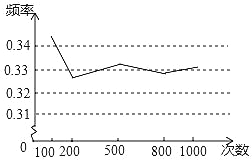
A. 掷一枚正六面体的骰子,出现1点朝上
B. 任意写一个整数,它能被2整除
C. 不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球
D. 先后两次掷一枚质地均匀的硬币,两次都出现反面
查看答案和解析>>
科目:初中数学 来源: 题型:
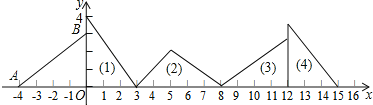
【题目】如图,在平面直角坐标系中,已知点![]() 、
、![]() ,对
,对![]() 连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第
连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第![]() 个三角形的直角顶点的坐标是______.
个三角形的直角顶点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )

A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com