
����Ŀ��(12��)��ͼ����Rt��ABC�У���ACB��90����AC��8��BC��6��CD��AB�ڵ�D.��P�ӵ�D���������߶�DC���C�˶�����Q�ӵ�C���������߶�CA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Cʱ�����㶼ֹͣ�����˶�ʱ��Ϊt�룮
(1)������CD�ij���
(2)����CPQ�����ΪS����S��t֮��ĺ�����ϵʽ����ȷ�����˶��������Ƿ����ijһʱ��t��ʹ��S��CPQ��S��ABC��9��100�������ڣ����t��ֵ���������ڣ�˵�����ɣ�
(3)��tΪ��ֵʱ����CPQΪ���������Σ�

���𰸡���1��4��8����2��t=![]() ��t=3����3��t=2��4���
��t=3����3��t=2��4���![]() ���
���![]() �룮
�룮
�������������������1�����ù��ɶ��������AB�������õȻ����Ϳ�����߶�CD�ij���
��2������P��PH��AC������ΪH��ͨ�����������Ƽ�����t�Ĵ���ʽ��ʾPH���Ӷ��������S��t֮��ĺ�����ϵʽ������![]() =9��100����t�ķ��̣��ⷽ�̼��ɽ�����⣮
=9��100����t�ķ��̣��ⷽ�̼��ɽ�����⣮
��3���ɷ���������������ۣ���CQ=CP�ɽ�������t�ķ��̣��Ӷ����t����PQ=PC��QC=QP����ֱ�ӵõ�����t�ķ��̣��ɽ����ڵ��������ε����ߺ�һ�����������ƣ����ɽ�������t�ķ��̣��Ӷ����t��
�����������1����ͼ1���ߡ�ACB=90����AC=8��BC=6��
��AB=10��
��CD��AB��
��S��ABC=![]() BC��AC=
BC��AC=![]() AB��CD��
AB��CD��
��CD=![]() =
=![]() =4.8��
=4.8��
���߶�CD�ij�Ϊ4.8��
��2��������P��PH��AC������ΪH����ͼ2��ʾ��
�����֪DP=t��CQ=t��
��CP=4.8��t��
�ߡ�ACB=��CDB=90����
���HCP=90�㩁��DCB=��B��
��PH��AC��
���CHP=90����
���CHP=��ACB��
���CHP�ס�BCA��
��![]() ��
��
��![]() ��
��
��PH= ![]() ��
��
��![]() =
=![]() CQ��PH=
CQ��PH=![]() t����
t����![]() ��=
��= ![]() ��
��
������ijһʱ��t��ʹ��![]() =9��100��
=9��100��
��![]() =
=![]() ��6��8=24����
��6��8=24����![]() =9��100��
=9��100��
����![]() ����24=9��100��
����24=9��100��
�����ã�5t2��24t+27=0��
����5t��9����t��3��=0��
��ã�t=![]() ��t=3��
��t=3��
��0��t��4.8��
����t=![]() ���t=3��ʱ��
���t=3��ʱ�� ![]() =9��100��
=9��100��
��3������
����CQ=CP����ͼ1��
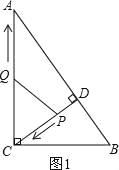
��t=4.8��t��
��ã�t=2.4��
����PQ=PC����ͼ2��ʾ��
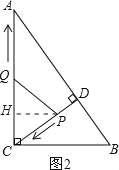
��PQ=PC��PH��QC��
��QH=CH=![]() QC=
QC=![]() ��
��
�ߡ�CHP�ס�BCA��
��![]() ��
��
��![]()
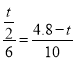 ��
��
��ã�t=![]() ��
��
����QC=QP��
����Q��QE��CP������ΪE����ͼ3��ʾ��
ͬ���ɵã�t=![]() ��
��
������������tΪ2.4���![]() ���
���![]() ��ʱ����CPQΪ���������Σ�
��ʱ����CPQΪ���������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�E��ֱ��AB��CD�ڲ�һ�㣬AB��CD������EA��ED��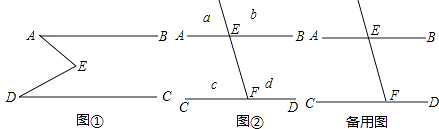
��1��̽�����룺
������A=20�㣬��D=40�㣬���AED=
�ڲ���ͼ���С�AED����EAB����EDC�Ĺ�ϵ���������ֲ�ͬ�ķ���֤����Ľ��ۣ�
��2����չӦ�ã�
��ͼ�ڣ�����FE��l1 �� l2���ڷֱ��ڵ�E��F��AB��CD��a��b��c��d�ֱ��DZ�����FE������4���������߽磬��������a��bλ��ֱ��AB�Ϸ���P��λ�������ĸ������ϵĵ㣬���룺��PEB����PFC����EPF�Ĺ�ϵ����д�����֣���ֱ��д�𰸣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���ǣ� ��
A. ��������������ƣ����Ӧ�ߵı����
B. ��������������ƣ����Ӧ�ǵıȵ��ڶ�Ӧ�ߵı�
C. ����������εĶ�Ӧ����ȣ������������������
D. ����������εĶ�Ӧ�ߵı���ȣ������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��AB��CD��EF��������O����AB��CD��OGƽ�֡�BOE�������EOG= ![]() ��AOE�����EOG�͡�DOF�Ķ�����
��AOE�����EOG�͡�DOF�Ķ����� 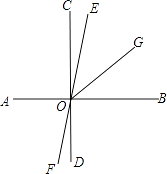
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD �� E ��CB �ӳ�����һ�㣬����������ȷ���ǣ� ��
A.�����1=��2 ����ôAB��CD
B.�����3=��4 ����ô AD��BC
C.���AD��BC �� ��ô��6+��BAD=180��.
D.�����6+��BCD=180�㣬��ôAD��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AB=5��AC=3����D��BC��һ���㣬����AD������ACD��AD�۵�����C���ڵ�C�䣬����C��D��AB�ڵ�E������BC�䣮����BC��D��ֱ��������ʱ��DE�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com