
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为_____.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
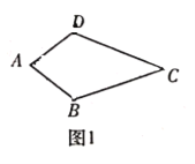
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
③神奇四边形的中点四边形是
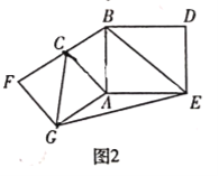
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
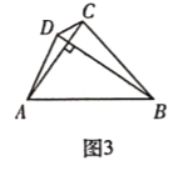
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、AC分别为⊙O的直径和弦,D为的中点,DE⊥AC于E,DE=6,AC=16.
(1)求证:DE是⊙O的切线.
(2)求直径AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与直线
与直线![]() 都经过
都经过![]() ,
,![]() 两点,该抛物线的顶点为
两点,该抛物线的顶点为![]() .
.
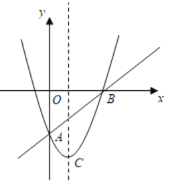
(1)求抛物线和直线![]() 的解析式;
的解析式;
(2)设点![]() 是直线
是直线![]() 下方抛物线上的一动点,求
下方抛物线上的一动点,求![]() 面积的最大值,并求
面积的最大值,并求![]() 面积最大时,点
面积最大时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示在矩形ABCD中,AB=6,AD=3,点E、F分别是边DC、DA的三等分点(DE![]() EC,DF
EC,DF![]() AF),四边形DFGE为矩形,连接BG.
AF),四边形DFGE为矩形,连接BG.
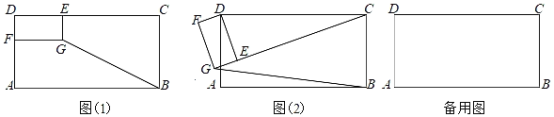
(1)问题发现:在图(1)中,![]() = ;
= ;
(2)拓展探究:将图(1)中的矩形DFGE绕点D旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图(2)的情形给出证明;
的大小有无变化?请仅就图(2)的情形给出证明;
(3)问题解决:当矩形DFGE旋转至B、G、E三点共线时,请直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;
(2)我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
①如图2,在□ABCD中,E为CD的中点,作BC的中点F;
②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH
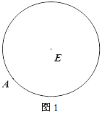
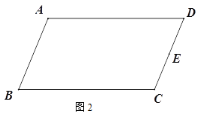
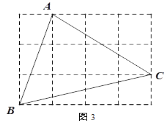
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
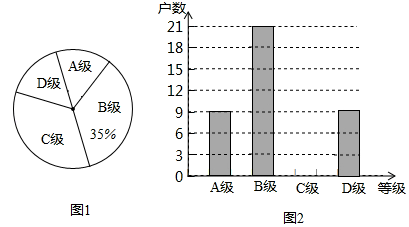
(1)本次抽样调查的养殖户的总户数是 ;把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?
(3)某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
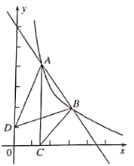
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF,连接CF交线段AB于点G,交AD于点H、连接EG.
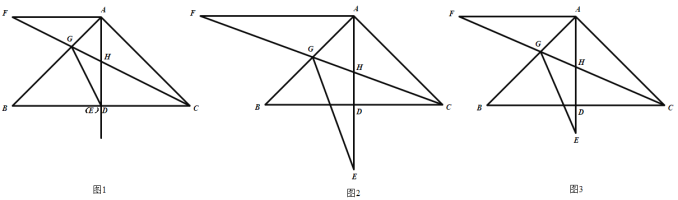
特例分析:
(1)如图1,当点E与点D重合时,“智敏”小组提出如下问题,请你解答:
①求证:AF=CD;
②用等式表示线段CG与EG之间的数量关系为:_______;
拓展探究:
(2)如图2,当点E在线段AD的延长线上,且DE=AD时,“博睿”小组发现CF=2EG.请你证明;
(3)如图3,当点E在线段AD的延长线上,且AE=AB时,![]() 的值为_______;
的值为_______;
推广应用:
(4)当点E在射线AD上运动时,![]() ,则
,则![]() 的值为______用含m.n的式子表示).
的值为______用含m.n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com