
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
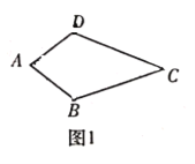
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
③神奇四边形的中点四边形是
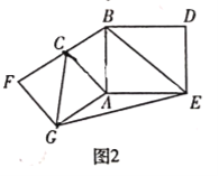
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
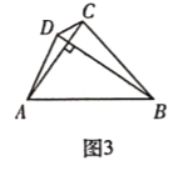
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
【答案】(1)菱形;真;矩形;(2)①见解析,②![]() ;(3)5
;(3)5
【解析】
(1)①根据神奇四边形的定义即可判断;
②连接AC、BD,根据SSS证明△ADC≌△ABC得出∠DAC=∠BAC,再利用等腰三角形三线合一的性质证明AC⊥BD即可得到结论;
③根据四边形对角线互相垂直,运用三角形中位线平行于第三边证明四个角都是直角,判断是矩形.
(2)①判断出CE⊥BG,即可得出四边形BCGE是神奇四边形;
②利用勾股定理即得出![]() ,再把相关数据代入求解即可;
,再把相关数据代入求解即可;
(3)利用勾股定理即可得出![]() ,把
,把![]() ,
,![]() 代入求得
代入求得![]() ,再由方程
,再由方程![]() 得到
得到![]() ,
,![]() ,进而得出
,进而得出![]() ,求解方程即可.
,求解方程即可.
![]() ①∵在平行四边形、矩形、菱形中,两条对角线互相垂直的四边形是菱形,
①∵在平行四边形、矩形、菱形中,两条对角线互相垂直的四边形是菱形,
∴菱形一定是神奇四边形;
故答案为:菱形;
②连接AC、BD,
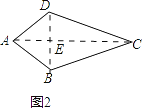
在△ACD和△ACB中,
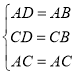
∴△ACD≌△ACB
∴∠DAC=∠BAC
∵AB=AD
∴AC⊥BD
∴四边形![]() 是神奇四边形.
是神奇四边形.
故答案为:真;
③如图:∵E、F、G、H分别为各边中点,
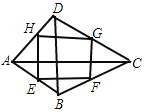
∴EF∥GH∥AC,EF=GH=![]() AC,
AC,
EH=FG=![]() DB,EH∥FG∥BD,
DB,EH∥FG∥BD,
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形.
故答案为:矩形;
![]() 证明:连接
证明:连接![]() 相交于点
相交于点![]() 交
交![]() 于点
于点![]() ,如图所
,如图所
![]() 正方形
正方形![]() 和正方形
和正方形![]() ,
,
![]() ,
,
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,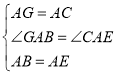
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]()
![]() 四边形
四边形![]() 是神奇四边形;
是神奇四边形;
②![]() 四边形
四边形![]() 是神奇四边形,
是神奇四边形,
![]() ,
,
![]()
由勾股定理得![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() 正方形
正方形![]() 和正方形
和正方形![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
![]() 四边形
四边形![]() 是神奇四边形,同
是神奇四边形,同![]() 中②的证明方法,可得
中②的证明方法,可得![]()
![]()
![]()
![]()
又![]() 分别是方程
分别是方程![]() 的两根.
的两根.
![]()
![]()
解得![]()
当![]() 时,不合题意,所以舍去,
时,不合题意,所以舍去,
![]()


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,连接OA、OB,若OA⊥OB,OB=OA,则k=_____.
的图象上,连接OA、OB,若OA⊥OB,OB=OA,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
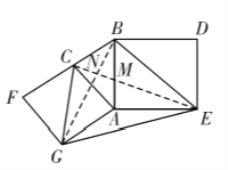
【题目】将两块直角三角板如图1放置,等腰直角三角板ABC的直角顶点是点A,AB=AC=3,直角板EDF的直角顶点D在BC上,且CD:BD=1:2,∠F=30°.三角板ABC固定不动,将三角板EDF绕点D逆时针旋转,旋转角为α(0°<α<90°).
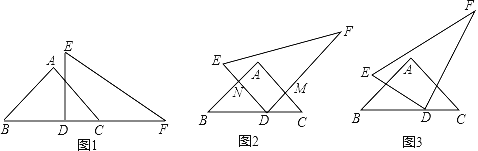
(1)当α= 时,EF∥BC;
(2)当α=45°时,三角板EDF绕点D逆时针旋转至如图2位置,设DF与AC交于点M,DE交AB于点N,求四边形ANDM的面积.
(3)如图3,设CM=x,四边形ANDM的面积为y,求y关于x的表达式(不用写x的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底4.4米的水平地面上立了一块警示牌
的距离为3.9米.同时为了提醒市民,在距离斜坡底4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成53°角时,测得信号塔
.当太阳光线与水平线成53°角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(tan53°≈1.3)( ).
的高约为(tan53°≈1.3)( ).
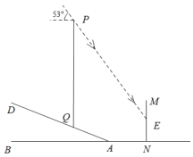
A.10.4B.11.9C.11.4D.13.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
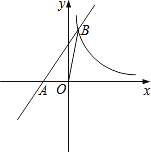
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 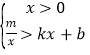 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)过A(-1,1),B(3,1),C(-2,y1),D(2,y2)四点,则y1与y2的大小关系是( )
A.y1>y2B.y1=y2C.y1<y2D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
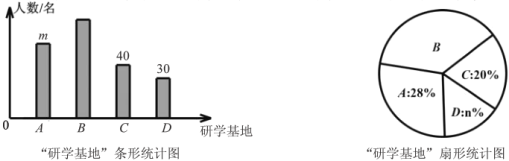
(1)统计图中![]() ______,
______,![]() ______;
______;
(2)若该校有1500名学生,请估计选择![]() 基地的学生人数;
基地的学生人数;
(3)某班在选择![]() 基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
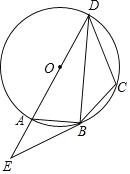
(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com