
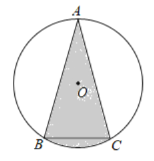
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,阴影部分的面积是( )
,阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接OB、OC,先利用同弧所对的圆周角等于所对的圆心角的一半,求出扇形的圆心角为60度,即可求出半径的长4,利用三角形和扇形的面积公式即可求解;
解:作OD⊥BC,则BD=CD,连接OB,OC,
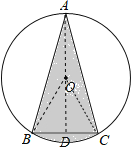
∴OD是BC的垂直平分线,
∵![]()
∴AB=AC,
∴A在BC的垂直平分线上,
∴A、O、D共线,
∵∠ACB=75°,AB=AC,
∴∠ABC=∠ACB=75°,
∴∠BAC=30°,
∴∠BOC=60°,
∵OB=OC,
∴△BOC是等边三角形,
∴OA=OB=OC=BC=4,
∵AD⊥BC,AB=AC,
∴BD=CD,
∴OD=2![]()
∴AD=4+2![]() ,
,
∴S△ABC=![]() BCAD=
BCAD=![]() ,
,
S△BOC=![]() BCOD=
BCOD=![]() ,
,
∴S阴影=S△ABC+S扇形BOC-S△BOC=![]() +
+![]()
=![]()
故选:A.


科目:初中数学 来源: 题型:
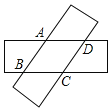
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为![]()
![]()
A. ![]() B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进旅游业的发展,某市新建一座景观桥.桥的拱肋ADB可视为抛物线的一部分,桥面AB可视为水平线段,桥面与拱肋用垂直于桥面的杆状景观灯连接,拱肋的跨度AB为40米,桥拱的最大高度CD为16米(不考虑灯杆和拱肋的粗细),求与CD的距离为5米的景观灯杆MN的高度.
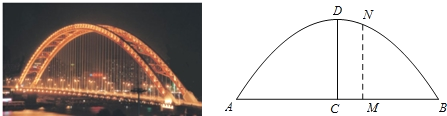
查看答案和解析>>
科目:初中数学 来源: 题型:
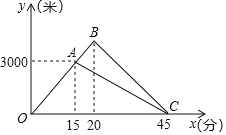
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
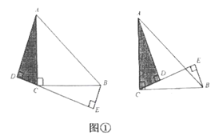
我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在![]() 中,
中,![]() ,
,![]() ,分别过
,分别过![]() 、
、![]() 向经过点
向经过点![]() 直线作垂线,垂足分别为
直线作垂线,垂足分别为![]() 、
、![]() ,我们很容易发现结论:
,我们很容易发现结论:![]() .
.
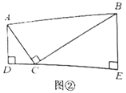

(1)探究问题:如果![]() ,其他条件不变,如图②,可得到结论;
,其他条件不变,如图②,可得到结论;![]() .请你说明理由.
.请你说明理由.
(2)学以致用:如图③,在平面直角坐标系中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且两直线夹角为
,且两直线夹角为![]() ,且
,且![]() ,请你求出直线
,请你求出直线![]() 的解析式.
的解析式.
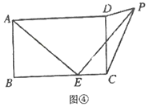
(3)拓展应用:如图④,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上—个动点,连接
边上—个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 落在点
落在点![]() 处,当点
处,当点![]() 在矩形
在矩形![]() 外部时,连接
外部时,连接![]() ,
,![]() .若
.若![]() 为直角三角形时,请你探究并直接写出
为直角三角形时,请你探究并直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
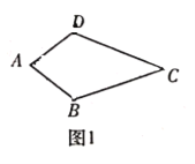
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
③神奇四边形的中点四边形是
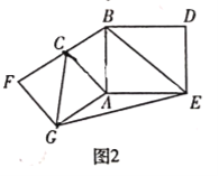
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
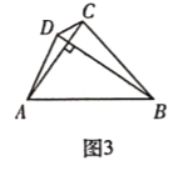
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状、大小完全相同的8×10方格纸,方格纸中的每个小正方形的边长均为1,点A,B,C均位于格点处,请按要求画出格点四边形(四边形各顶点都在格点上).
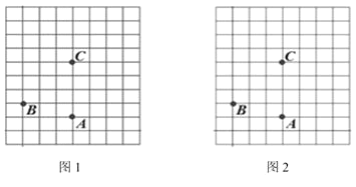
(1)在图1中画出一个以点A,B,C,P为顶点的格点四边形,且为中心对称图形.
(2)在图2中画出一个以点A,B,C,Q为顶点的格点四边形,AC平分∠BCQ,且有两个内角为90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
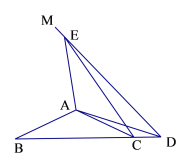
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
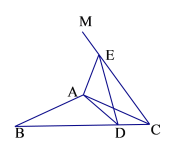
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com