
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
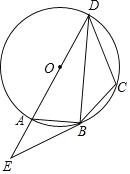
(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)详见解析;(2)OA=![]() .
.
【解析】
(1)连接OB,证明∠ABE=∠ADB,可得∠ABE=∠BDC,则∠ADB=∠BDC;
(2)证明△AEB∽△CBD,AB=x,则BD=2x,可求出AB,则答案可求出.
(1)证明:连接OB,
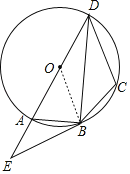
∵BE为⊙O的切线,
∴OB⊥BE,
∴∠OBE=90°,
∴∠ABE+∠OBA=90°,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠ABE+∠OAB=90°,
∵AD是⊙O的直径,
∴∠OAB+∠ADB=90°,
∴∠ABE=∠ADB,
∵四边形ABCD的外接圆为⊙O,
∴∠EAB=∠C,
∵∠E=∠DBC,
∴∠ABE=∠BDC,
∴∠ADB=∠BDC,
即DB平分∠ADC;
(2)解:∵tan∠ABE=![]() ,
,
∴设AB=x,则BD=2x,
∴![]() ,
,
∵∠BAE=∠C,∠ABE=∠BDC,
∴△AEB∽△CBD,
∴![]() ,
,
∴![]() ,
,
解得x=3![]() ,
,
∴AB=![]() x=15,
x=15,
∴OA=![]() .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
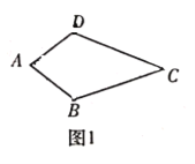
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
③神奇四边形的中点四边形是
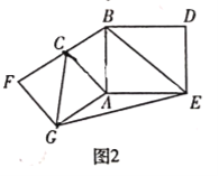
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
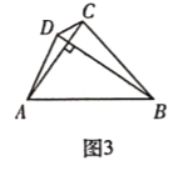
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A.顺次联结任意四边形四边中点所得的四边形是平行四边形
B.顺次联结对角线相等的四边形四边中点所得的四边形是菱形
C.顺次联结对角线互相垂直的四边形四边中点所得的四边形是矩形
D.顺次联结两组邻边互相垂直的四边形四边中点所得的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
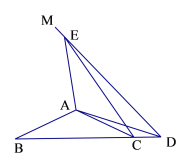
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
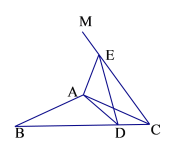
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
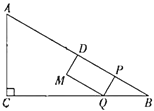
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位向终点
个单位向终点![]() 匀速运动(点
匀速运动(点![]() 不与
不与![]() 、
、![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() .以
.以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)直接写出![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形不是矩形时,求
重叠部分图形不是矩形时,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)沿直线![]() 将矩形
将矩形![]() 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
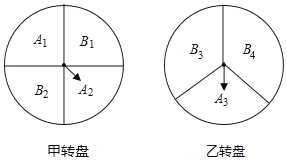
【题目】某超市在春节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣和优惠,在每个转盘中指针指向每个区域的可能性均相同,若指针指向分界线,则重新转动转盘,区域对应的优惠方式如下,A1,A2,A3区域分别对应9折8折和7折优惠,B1,B2,B3,B4区域对应不优惠?本次活动共有两种方式.
方式一:转动转盘甲,指针指向折扣区域时,所购物品享受对应的折扣优惠,指针指向其他区域无优惠;
方式二:同时转动转盘甲和转盘乙,若两个转盘的指针均指向折扣区域时,所购物品享受折上折的优惠,其他情况无优惠.
(1)若顾客选择方式一,则享受优惠的概率为 ;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能顾客享受折上折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
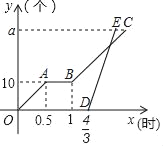
【题目】甲、乙两名工人分别加工a个同种零件.甲先加工一段时间,由于机器故障进行维修后继续按原来的工作效率进行加工,当甲加工![]() 小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
(1)甲的工作效率为 个/时,维修机器用了 小时
(2)乙的工作效率是 个/时;问题解决:
①乙加工多长时间与甲加工的零件数量相同,并求此时乙加工零件的个数;
②若乙比甲早10分钟完成任务,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
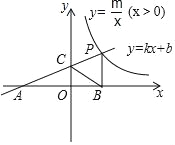
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<![]() 的x的取值范围;
的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc<0;②b2-4ac<0;③3a+c<0;④m为任意实数,则m(am-b)+b≤a;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=-2,其中正确的有______(只填序号).
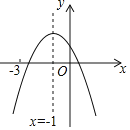
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com