
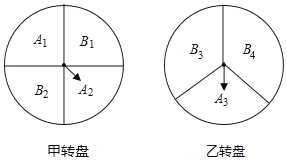
����Ŀ��ij�����ڴ����ڼ俪չ�Żݻ���������߿���ͨ��ת��ת�̵ķ�ʽ�����ۿۺ��Żݣ���ÿ��ת����ָ��ָ��ÿ������Ŀ����Ծ���ͬ����ָ��ָ��ֽ��ߣ�������ת��ת�̣������Ӧ���Żݷ�ʽ���£�A1��A2��A3����ֱ��Ӧ9��8�ۺ�7���Żݣ�B1��B2��B3��B4�����Ӧ���Żݣ����λ�������ַ�ʽ��
��ʽһ��ת��ת�̼ף�ָ��ָ���ۿ�����ʱ��������Ʒ���ܶ�Ӧ���ۿ��Żݣ�ָ��ָ�������������Żݣ�
��ʽ����ͬʱת��ת�̼�ת���ң�������ת�̵�ָ���ָ���ۿ�����ʱ��������Ʒ���������۵��Żݣ�����������Żݣ�
��1�����˿�ѡ��ʽһ���������Żݵĸ���Ϊ�� ����
��2�����˿�ѡ��ʽ����������״ͼ���б����г����п��ܹ˿������������Żݵĸ��ʣ�
 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
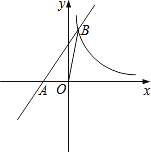
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����x�ύ�ڵ�A����1��0�����뷴��������y= ![]() �ڵ�һ�����ڵ�ͼ���ڵ�B��
�ڵ�һ�����ڵ�ͼ���ڵ�B��![]() ��n��������OB����S��AOB=1��
��n��������OB����S��AOB=1��
��1������������һ�κ����Ĺ�ϵʽ��
��2��ֱ��д������ʽ�� 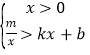 �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���㣻��
���㣻��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ����
����![]() ������Ϊ
������Ϊ![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ������ȷ�Ľ��۸�����(����)
������ȷ�Ľ��۸�����(����)
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
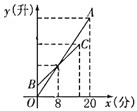
����Ŀ��һ����ˮ���мס�������עˮ�ܺ�һ����ˮ�ܱ�������ˮ�ܾ��ѹرգ���֪��עˮ�ܵ�עˮ�ٶ�Ϊ10��/�֣��ȴ���עˮ��4���ӣ��ٴ�עˮ�ܣ��ס�������ˮ�ܾ�עˮ20���ӣ����עˮ�ܵĹ���ʱ��Ϊ![]() ���֣�����עˮ�ܵ�עˮ��
���֣�����עˮ�ܵ�עˮ��![]() ��������ʱ��
��������ʱ��![]() ���֣��ĺ���ͼ��Ϊ�߶�
���֣��ĺ���ͼ��Ϊ�߶�![]() ����עˮ�ܵ�עˮ��
����עˮ�ܵ�עˮ��![]() ��������ʱ��
��������ʱ��![]() ���֣��ĺ���ͼ��Ϊ�߶�
���֣��ĺ���ͼ��Ϊ�߶�![]() ����ͼ��ʾ��
����ͼ��ʾ��
��1�����עˮ�ܵ���עˮ����
��2�����߶�![]() ����Ӧ�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
����Ӧ�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3����עˮ�ܴ�16���Ӻ���ˮ�ܣ���֪��ˮ�ܱ�����ˮ�ٶ�Ϊ20��/�֣������ˮ�ܴʱ���ܽ���ˮ�ص�ˮ�ſգ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����ԲΪ��O��AD����O��ֱ��������B����O�����ߣ���DA���ӳ����ڵ�E������BD���ҡ�E����DBC��
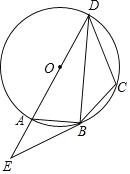
��1����֤��DBƽ�֡�ADC��
��2����EB��10��CD��9��tan��ABE��![]() ������O�İ뾶��
������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1����С�������������������˲���̤���ϣ���ס���֣�����·һ��̧�ȣ��ͻ����̤������������ת���Ӳ��濴ͼ2������DE��1.7m��AD��0.3m��̤�徲ֹʱ�Ӳ��濴��AE�ϵ�B�غϣ�BE��0.2m����̤����ת��C��ʱ����á�CAB=42�������ʱ��C�������EF�ĸ߶ȣ��������ȷ��0.1m�����ο����ݣ�sin42��=0.67��cos42��=0.74��tan42��=0.90��
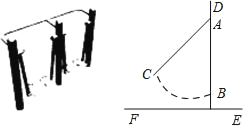
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ϊ�˰�ȫ��������������ͼ��һ����·����ͨ������ijֱ��·��MN����60ǧ��/Сʱ��Ϊ�˼����Ƿ��٣��ڹ�·MN�������˹۲��C���ӹ۲��C���һС���ӵ�A�����B��ʻ��5���ӣ���֪��CAN=45�㣬��CBN=60�㣬BC=200�ף��˳�����������˵�����ɣ�
���ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
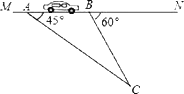
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��һ��Բ��ֽƬ�ϼ���һ��Բ�Ľ�Ϊ90�������ABC,ʹ��A��B��C��Բ����,�����µ�������Ϊһ��Բ����,���Բ�ĸ�Ϊ![]() ,�����Բ��ֽƬ��ֱ��Ϊ( )
,�����Բ��ֽƬ��ֱ��Ϊ( )
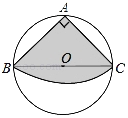
A. 12cm B. 20cm C. 24cm D. 28cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
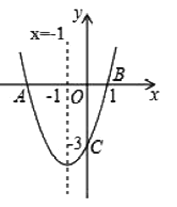
����Ŀ����ͼ����֪������y=ax2+bx��2��a��0����x�ύ��A��B���㣬��y�ύ��C�㣬ֱ��BD���������ڵ�D������D��2��3����tan��DBA=![]() ��
��
��1���������ߵĽ���ʽ��
��2����֪��MΪ��������һ���㣬���ڵ������ޣ�˳�����ӵ�B��M��C��A�����ı���BMCA��������ֵ��
��3���ڣ�2�����ı���BMCA������������£�����M��ֱ��ƽ����y�ᣬ������ֱ�����Ƿ����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��AC���е�Բ�������ڣ����Բ��Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com