
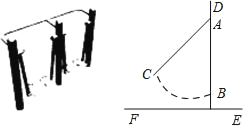
ЁОЬтФПЁПЭМ1жаЪЧаЁЧјГЃМћЕФТўВНЛњЃЌЕБШЫВШдкЬЄАхЩЯЃЌЮезЁЗіЪжЃЌЯёзпТЗвЛбљЬЇЭШЃЌОЭЛсДјЖЏЬЄАхСЌИЫШЦжса§зЊЃЌДгВрУцПДЭМ2ЃЌСЂжљDEИп1.7mЃЌADГЄ0.3mЃЌЬЄАхОВжЙЪБДгВрУцПДгыAEЩЯЕуBжиКЯЃЌBEГЄ0.2mЃЌЕБЬЄАха§зЊЕНCДІЪБЃЌВтЕУЁЯCAB=42ЁуЃЌЧѓДЫЪБЕуCОрРыЕиУцEFЕФИпЖШЃЎЃЈНсЙћОЋШЗЕН0.1mЃЉЃЈВЮПМЪ§ОнЃКsin42Ёу=0.67ЃЌcos42Ёу=0.74ЃЌtan42Ёу=0.90ЃЉ
ЁОД№АИЁП0.5
ЁОНтЮіЁП
ИљОнЬтвтЕУГіAC=AB=1.2mЃЌЙ§ЕуCзїCGЁЭABгкGЃЌЙ§ЕуCзїCHЁЭEFгкЕуHЃЌИљОнRtЁїACGЕФШ§НЧКЏЪ§жЕЧѓГіAGЕФГЄЖШЃЌДгЖјЕУГіEGЕФГЄЖШЃЌИљОнОиаЮЕФаджЪЕУГіCH=EGЃЎ
гЩЬтвтЃЌЕУAE=DEЉAD=1.7Љ0.3=1.4mЃЌAB=AEЉBE=1.4Љ0.2=1.2mЃЌ
гЩа§зЊЃЌЕУAC=AB=1.2mЃЌЙ§ЕуCзїCGЁЭABгкGЃЌЙ§ЕуCзїCHЁЭEFгкЕуHЃЌ
дкRtЁїACGжаЃЌЁЯAGC=90ЁуЃЌЁЯCAG=42ЁуЃЌ cosЁЯCAG=![]() ЃЌ
ЃЌ
ЁрAG=ACcosЁЯCAG=1.2ЁСcos42Ёу=1.2ЁС0.74Ёж0.9mЃЌ
ЁрEG=AEЉAGЁж1.4Љ0.9=0.5mЃЌЁрCH=EG=0.5mЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯABC=25ЁуЃЌOЮЊABЕФжаЕу. НЋOAШЦЕуOФцЪБеыа§зЊІШ ЁужСOPЃЈ0<ІШ<180ЃЉЃЌЕБЁїBCPЧЁЮЊжсЖдГЦЭМаЮЪБЃЌІШЕФжЕЮЊ_____________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
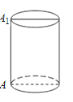
ЁОЬтФПЁПШчЭМЃЌгавЛФОжЪдВжљБЪЭВЕФИпЮЊ9cmЃЌЕзУцАыОЖЮЊ2cm,ЯжвЊЮЇШЦБЪЭВЕФБэУцгЩAЕНA1(A,A1дкдВжљЕФЭЌвЛжсНиУцЩЯ)ЯтЩЯвЛЬѕвјЩЋН№ЪєЯпзїЮЊзАЪЮЃЌдђетЬѕН№ЪєЯпЕФзюЖЬГЄЖШЪЧ_________cm.(ІаШЁ3)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
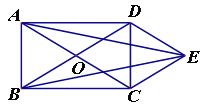
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌDEЁЮACЃЌCEЁЮBD.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮOCEDЮЊСтаЮЃЛ
ЃЈ2ЃЉСЌНгAEЁЂBEЃЌAEгыBEЯрЕШТ№ЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
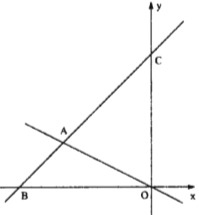
ЁОЬтФПЁПШчЯТЭМЫљЪОЃЌжБЯпyЃНЃ![]() xЃЋ3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЌгыжБЯпyЃНxНЛгкЕуCЃЌЯпЖЮOAЩЯЕФЕуQвдУПУы1ИіЕЅЮЛЕФЫйЖШДгЕуOГіЗЂЯђЕуAзїдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНсCQ.
xЃЋ3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЌгыжБЯпyЃНxНЛгкЕуCЃЌЯпЖЮOAЩЯЕФЕуQвдУПУы1ИіЕЅЮЛЕФЫйЖШДгЕуOГіЗЂЯђЕуAзїдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНсCQ.
(1)ЧѓГіЕуCЕФзјБъЃЛ
(2)ШєЁїOQCЪЧЕШбќжБНЧШ§НЧаЮЃЌдђtЕФжЕЮЊ________ЃЛ
(3)ШєCQЦНЗжЁїOACЕФУцЛ§ЃЌЧѓжБЯпCQЖдгІЕФКЏЪ§БэДяЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋГЄЗНаЮжНЦЌABCDелЕўЃЌЪЙБпDCТфдкЖдНЧЯпACЩЯЃЌелКлЮЊCEЃЌЧвDЕуТфдкЖдНЧЯпDЁфДІЃЎШєAB=3ЃЌAD=4ЃЌдђEDЕФГЄЮЊ

AЃЎ![]() BЃЎ3 CЃЎ1 DЃЎ
BЃЎ3 CЃЎ1 DЃЎ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() КЭЩфЯп
КЭЩфЯп![]() ЩЯдЫЖЏ.
ЩЯдЫЖЏ.
(1)ЧѓжБЯп![]() ЕФБэДяЪН.
ЕФБэДяЪН.
(2)Чѓ![]() ЕФУцЛ§.
ЕФУцЛ§.
(3)жБНгаДГіЪЙ![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЕФЕу
ЕФЕу![]() зјБъ.
зјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЪЧ
ЪЧ![]() ЕФШ§ЬѕФкНЧЦНЗжЯпЃЎФЧУДЃЌ
ЕФШ§ЬѕФкНЧЦНЗжЯпЃЎФЧУДЃЌ![]() ЕФУцЛ§ЕШгк________ЃЎ
ЕФУцЛ§ЕШгк________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯёгы
ЕФЭМЯёгы![]() жсНЛгкЕуAЃЌгы
жсНЛгкЕуAЃЌгы![]() жсНЛгкЕуBЃЌЕуCЪЧжБЯпABЩЯвЛЕуЃЌЫќЕФзјБъЮЊ(
жсНЛгкЕуBЃЌЕуCЪЧжБЯпABЩЯвЛЕуЃЌЫќЕФзјБъЮЊ(![]() ЃЌ2)ЃЌОЙ§ЕуCзїжБЯпCDЁЮжсНЛ
ЃЌ2)ЃЌОЙ§ЕуCзїжБЯпCDЁЮжсНЛ![]() жсгкЕуD.
жсгкЕуD.
(1)ЧѓЕуCЕФзјБъМАЯпЖЮABЕФГЄЃЛ
(2)вбжЊЕуPЪЧжБЯпCDЩЯвЛЕу.
ЂйШєЁїPOCЕФУцЛ§ЪЧ4ЃЌЧѓЕуPЕФзјБъЃЛ
ЂкШєЁїPOCЪЧжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФЕуPЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com