
【题目】如图,平面直角坐标系中,一次函数![]() 的图像与
的图像与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,点C是直线AB上一点,它的坐标为(
轴交于点B,点C是直线AB上一点,它的坐标为(![]() ,2),经过点C作直线CD∥轴交
,2),经过点C作直线CD∥轴交![]() 轴于点D.
轴于点D.
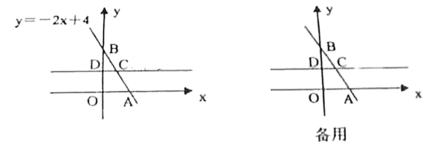
(1)求点C的坐标及线段AB的长;
(2)已知点P是直线CD上一点.
①若△POC的面积是4,求点P的坐标;
②若△POC是直角三角形,请直接写出所有满足条件的点P的坐标.
【答案】(1)C(1,2),![]() ;(2)①(-2,2)或(6,2);② (0,2)或(-4,2)
;(2)①(-2,2)或(6,2);② (0,2)或(-4,2)
【解析】
(1)把(m,2)代入![]() 求出m的值,即可求出点C坐标,求出A、B两点坐标,利用勾股定理即可求出AB的长;
求出m的值,即可求出点C坐标,求出A、B两点坐标,利用勾股定理即可求出AB的长;
(2)①利用三角形的面积公式求出PC的长即可解决问题,注意两解;
②分两种情形讨论即可①P是直角顶点,②O是直角顶点.
解:(1)把(m,2)代入![]() 得-2m+4=2,
得-2m+4=2,
∴m=1,
∴C(1,2),
当x=0时,y=4;
当y=0时,-2x+4=0,即x=2,
∴OA=2,OB=4,
在Rt△AOB中,OA=2,OB=4,
∴AB=![]() .
.
(2)①∵OD⊥CP,
∴△POC的高是2,
∴S△POC=![]() CPOD=4,
CPOD=4,
∵OD=2,
∴CP=4,
∴P点坐标是(-2,2)或(6,2).
②∵∠OCP一定不是直角,
∴当∠OPC=90°时,点P恰好在点D,
∴P1(0,2).
设直线OC的解析式为y=kx,
把C(1,2)代入得
k=2,
∴k=2,
y=2x,
∴直线OP的解析式为y=-![]() x,
x,
∴y=2时,x=-4,
∴P2(-4,2).
∴P点坐标是(0,2)或(-4,2).


科目:初中数学 来源: 题型:
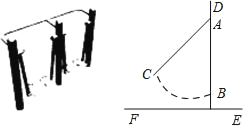
【题目】图1中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°,求此时点C距离地面EF的高度.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PA+PB的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
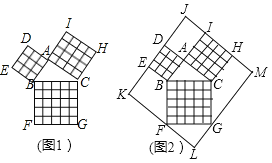
A.120B.110C.100D.90
查看答案和解析>>
科目:初中数学 来源: 题型:
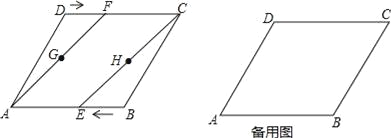
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是______________.(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
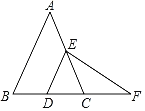
【题目】如图,在△ABC中,AB=AC,DE∥AB,分别交BC、AC于点D、E,点F在BC的延长线上,且CF=DE.
(1)求证:△CEF是等腰三角形;
(2)连接AD,当AD⊥BC,BC=8,△CEF的周长为16时,求△DEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠BAC=90°,AB=AC,∠ADB=45°

(1)求证:BD⊥CD;
(2)若BD=6,CD=2,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“快乐分式”.如:![]() ,则
,则 ![]() 是“快乐分式”.
是“快乐分式”.
(1)下列式子中,属于“快乐分式”的是 (填序号);
①![]() ,②
,② ![]() ,③
,③![]() ,④
,④ ![]() .
.
(2)将“快乐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() = .
= .
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com