
【题目】勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
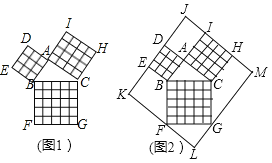
A.120B.110C.100D.90
【答案】B
【解析】
延长AB交KF于点O,延长AC交GM于点P,可得四边形AOLP是正方形,然后求出正方形的边长,再求出矩形KLMJ的长与宽,然后根据矩形的面积公式列式计算即可得解.
解:延长AB交KF于点O,延长AC交GM于点P,如图所示:
则四边形OALP是矩形.
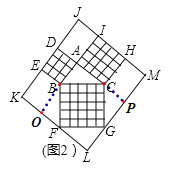
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵Rt△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,
∵∠BAC=∠BOF,
∠ACB=∠OBF,
BC=BF,,
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
∴矩形AOLP是正方形,边长AO=AB+AC=3+4=7,
∴KL=3+7=10,LM=4+7=11,
∴长方形KLMJ的面积为10×11=110.
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
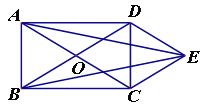
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列五个命题中的真命题有( )
①两条直线被第三条直线所截,同位角相等;②三角形的一个外角等于它的两个内角之和;③两边分别相等且一组内角相等的两个三角形全等;④有理数与数轴上的点一一对应;⑤实数分为有理数、无理数.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购这两种原料的价格如下表:
甲 | 乙 | |
维生素C(单位/千克) | 600 | 100 |
原料价格(元/千克) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元.请问:既要符合要求又要成本最低,则购买甲种原料应该在什么范围之内,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为
是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为![]() ,所以可用、
,所以可用、![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是__________,小数部分是__________.
的整数部分是__________,小数部分是__________.
(2)如果![]() 的整数部分为
的整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知![]() ,其中
,其中![]() 是整数,且
是整数,且![]() .则求
.则求![]() 的平方根的值.
的平方根的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数![]() 的图像与
的图像与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,点C是直线AB上一点,它的坐标为(
轴交于点B,点C是直线AB上一点,它的坐标为(![]() ,2),经过点C作直线CD∥轴交
,2),经过点C作直线CD∥轴交![]() 轴于点D.
轴于点D.
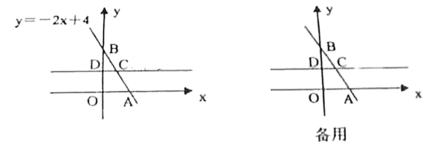
(1)求点C的坐标及线段AB的长;
(2)已知点P是直线CD上一点.
①若△POC的面积是4,求点P的坐标;
②若△POC是直角三角形,请直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC,AC=![]() .四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积为( )
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积为( )
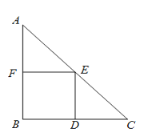
A.25.B.![]() .C.5.D.10.
.C.5.D.10.
查看答案和解析>>
科目:初中数学 来源: 题型:
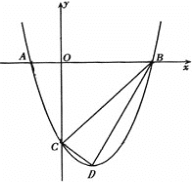
【题目】如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com