
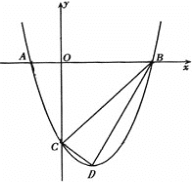
【题目】如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
【答案】(1)y=x2-2x-3 顶点是(1,-4);(2)直角三角形;(3)点P在该抛物线上滑动至(![]() ,4)或(
,4)或(![]() ,4)或(1,-4)时,满足S⊿PAB=8.
,4)或(1,-4)时,满足S⊿PAB=8.
【解析】
(1)设抛物线的解析式为y=ax2+bx+c,把A、B、C、三点坐标代入求出a、b、c的值即可得答案.(2)过点D分别作x轴、y轴的垂线,垂足分别为E、F,根据B、C、D三点的坐标可求出BD、CD、BC的长,根据三边的长即可判断△BCD的形状.(3)设P的纵坐标为![]() ,利用三角形面积可求出P点的纵坐标,代入解析式可求出横坐标即可.
,利用三角形面积可求出P点的纵坐标,代入解析式可求出横坐标即可.
(1)设抛物线解析式为y=ax2+bx+c
∴依题意得: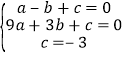 解得
解得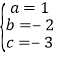
∴抛物线解析式为:y=x2-2x-3 顶点是(1,-4)
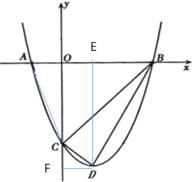
(2)以B、C、D为顶点的三角形是直角三角形。
过点D分别作x轴、y轴的垂线,垂足分别为E、F
在Rt⊿BOC中,OB=3,OC=3,
∴BC2=18
在Rt⊿CDF中,DF=1,CF=OF-OC=4-3=1
CD2=2
在Rt⊿BDE中,DE=4,BE=OB-OE=3-1=2,
∴BD2=20
∴BC2+CD2=BD2,故⊿BCD为直角三角形。
(3)设P的纵坐标为![]()
∵S⊿PAB=8
∴![]() AB·
AB·![]() =8
=8
∵AB=3+1=4
∴![]() =4
=4
∴yp=![]()
把yp=4代入解析式得4=x2-2x-3,解得:x=![]()
把yp=-4代入解析式得-4=x2-2x-3,解得:x=1
∴点P在该抛物线上滑动至(![]() ,4)或(
,4)或(![]() ,4)或(1,-4)时,满足S⊿PAB=8
,4)或(1,-4)时,满足S⊿PAB=8


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
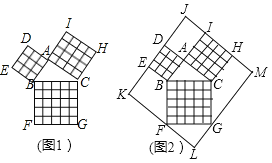
【题目】勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
A.120B.110C.100D.90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠BAC=90°,AB=AC,∠ADB=45°

(1)求证:BD⊥CD;
(2)若BD=6,CD=2,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与正比例函数
的图像与正比例函数![]() 的图像都经过点
的图像都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 在正比例函数
在正比例函数![]() 的图像上.
的图像上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象进行以下探究:
⑴请问甲乙两地的路程为 ;
⑵求慢车和快车的速度;
⑶求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
⑷如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图像.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“快乐分式”.如:![]() ,则
,则 ![]() 是“快乐分式”.
是“快乐分式”.
(1)下列式子中,属于“快乐分式”的是 (填序号);
①![]() ,②
,② ![]() ,③
,③![]() ,④
,④ ![]() .
.
(2)将“快乐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() = .
= .
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列步骤是一位同学在解方程![]() =3时的解答过程:
=3时的解答过程:
方程两边都乘以x,得x﹣1+2=3(第一步)
移项,合并同类项,得x=2(第二步)
经检验,x=2是原方程的解(第三步)
所以原方程的解是:x=2(第四步)
(1)他的解答过程是从第 步开始出错的,出错原因是 ;
(2)请写出此题正确的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com