练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

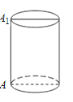
    【题目】如图，有一木质圆柱笔筒的高为9cm，底面半径为2cm,现要围绕笔筒的表面由A到A1(A,A1在圆柱的同一轴截面上)镶上一条银色金属线作为装饰，则这条金属线的最短长度是_________cm.(π取3)

    【答案】15

    【解析】

    这道题主要考查的是几何体的展开图，灵活运用圆柱的侧面展开图是矩形和两点之间线段最短，是解决本题的关键.立体图形中的最短距离，通常要转换为平面图形的两点间的线段长来进行解决.

    1、这是一道利用圆柱的展开图解决问题的题目，圆柱的侧面展开图是长方形；

    2、可沿母线 将圆柱展开得一个长方形，长方形的长是圆柱的底面周长，宽是圆柱的高；

    3、要围绕笔筒的表面由A到A1，根据两点之间线段最短即可解答此题.

    解：根据图示，展开图对角线的长度就是这条金属线的最短长度，

    故答案为：15.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰RtABC 中，∠BAC=90°，在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连接PC，若△ABC的面积为8cm2，则△BPC的面积为（ ）

    A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线 y ax2 2a（x a＜0）位于 x 轴上方的图象记为F1，它与 x 轴交于 P1、O 两点，图象 F2与F1关于原点 O 对称， F2 与 x 轴的另一个交点为 P2 ， F1 将与 F2 同时沿 x 轴向右平移 P1 P2 的长度即可得到F3与F4 ；再将 F3与F4 同时沿 x 轴向右平移 P1 P2 的长度即可得到 F5与F6 ；…；按这样的方式一直平移下去即可得到一系列图象 F1，F2，，Fn ．我们把这组图象称为“波浪抛物线”．

    （1）当 a=﹣1 时，

    ①求 F1 图象的顶点坐标；

    ②点 H（2014，﹣3） （填“在”或“不在”）该“波浪抛物线”上；若图象 F n的顶点 T n的横坐标为201，则图象 F n对应的解析式为 ， 其自变量 x 的取值范围为 .

    （2）设图象 Fn、Fn+1 的顶点分别为 Tn、Tn+1 （n 为正整数），x 轴上一点 Q 的坐标为（12，0）．试探究： 当 a 为何值时，以 O、 Tn、Tn+1 、Q 四点为顶点的四边形为矩形？并直接写出此时 n 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲车从A地到B地，乙车从B地到A地，乙车先出发先到达，甲乙两车之间的距离y（千米）与行驶的时间x（小时）的函数关系如图所示，则下列说法中不正确的是（　　）

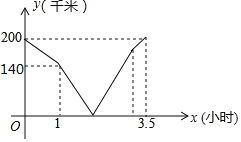
    A.甲车的速度是80km/hB.乙车的速度是60km/h

    C.甲车出发1h与乙车相遇D.乙车到达目的地时甲车离 B地10km

    查看答案和解析>>

    科目：初中数学 来源： 题型：

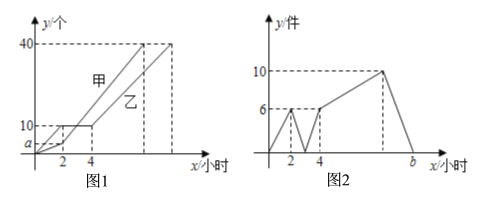
    【题目】甲、乙两人分别安装同一种零件40个，其中乙在安装两小时后休息了2小时，后继续按原来进度工作，他们每人安装的零件总数y（个）与安装时间x（小时）的函数关系如图1所示，两人安装零件总数之差z（件）与时间x（小时）的函数关系如图2所示．

    （1）a＝　 　；b＝　 　．

    （2）求出甲工作2小时后的安装的零件数y与时间x的函数关系．

    （3）甲、乙两人在什么时间生产的零件总数相差8个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．

    （1）求证：CE=CF；

    （2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

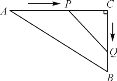
    【题目】如图，在△ABC中，AC＝50 cm，BC＝40 cm，∠C＝90°，点P从点A开始沿AC边向点C以2 cm/s的速度匀速移动，同时另一点Q从点C开始以3 cm/s的速度沿着射线CB匀速移动，当△PCQ的面积等于300 cm2时，运动时间为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

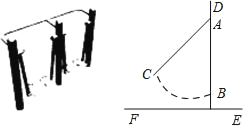
    【题目】图1中是小区常见的漫步机，当人踩在踏板上，握住扶手，像走路一样抬腿，就会带动踏板连杆绕轴旋转，从侧面看图2，立柱DE高1.7m，AD长0.3m，踏板静止时从侧面看与AE上点B重合，BE长0.2m，当踏板旋转到C处时，测得∠CAB=42°，求此时点C距离地面EF的高度．（结果精确到0.1m）（参考数据：sin42°=0.67，cos42°=0.74，tan42°=0.90）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长度为1个单位长度的小正方形组成的正方形中，点A，B，C在小正方形的顶点上．

    （1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′

    （2）三角形ABC的面积为　 　；

    （3）在直线l上找一点P，使PA+PB的长最短．

    查看答案和解析>>

    同步练习册答案