
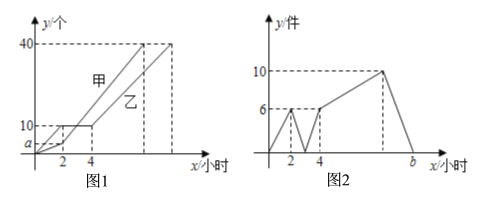
����Ŀ���ס������˷ֱ�װͬһ�����40�����������ڰ�װ��Сʱ����Ϣ��2Сʱ���������ԭ�����ȹ���������ÿ�˰�װ���������y�������밲װʱ��x��Сʱ���ĺ�����ϵ��ͼ1��ʾ�����˰�װ�������֮��z��������ʱ��x��Сʱ���ĺ�����ϵ��ͼ2��ʾ��
��1��a���� ����b���� ����
��2���������2Сʱ��İ�װ�������y��ʱ��x�ĺ�����ϵ��
��3���ס���������ʲôʱ������������������8����
���𰸡���1��4�� 10����2��y��6x��8��2��x��8������3��6Сʱ��8.4Сʱ.
��������
��1������ͼ����a��ֵ��ͼ1��֪4Сʱ��һֱ�������ȣ���������ɣ�����ֻ�е���Ҳ�������ʱ�����˰�װ�������֮��Ż�Ϊ0�������ҵĹ���Ч�ʼ������b��ֵ��
��2������ͼ���������2Сʱ���ͼ����![]() �͵�
�͵�![]() ���ô���ϵ�������ɵã�
���ô���ϵ�������ɵã�
��3������ͼ��������4Сʱ������������������Ŵﵽ8�����ٸ��ݼס��ҵĹ���Ч�ʣ�����ڼ��������֮ǰ�ͼ��������֮����������������г���ʽ��⼴��.
��1����ͼ�ɵã�![]() ��
��
ͼ1��֪4Сʱ��һֱ�������ȣ���������ɣ�����ֻ�е���Ҳ�������ʱ�����˰�װ�������֮��Ż�Ϊ0���ҵĹ���Ч��Ϊ![]() ��/Сʱ��
��/Сʱ��
��![]() ��
��
��2������4Сʱ���˰�װ�������֮��ɵã�4Сʱ�װ�װ���������Ϊ![]() ����
����
�����2Сʱ��İ�װ�������y��ʱ��x�ĺ�����ϵ��![]() ��
��
����2Сʱ��İ�װ�������y��ʱ��x�ĺ���ͼ�����![]() �͵�
�͵�![]() ��
��
�����![]() �����
�����![]() ��
��
![]()
��![]() ��
��![]() �����
�����![]() ��
��
�ʼ���2Сʱ��İ�װ�������y��ʱ��x�ĺ�����ϵ��![]() ��
��
��3����tСʱ�ס�����������������������8����
��ͼ2��![]() ��
��
2Сʱ��Ĺ���Ч��Ϊ��![]() ��/Сʱ��
��/Сʱ��
���ڼ����֮ǰ����![]() ʱ��
ʱ��![]()
���![]() ��
��
���ڼ����֮��![]() ʱ��
ʱ��![]() ��
��
���![]()
�𣺼ס���������6Сʱ��8.4Сʱʱ����������������8��.


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и�ʽ��Ȼ��ش�����
(x+4)(x+3)=
(x+4)(x-3)=
(x-4)(x+3)=
(x-4)(x-3)=
��1���������ʽ�ܽ���ɣ�һ��أ�(x+p)(x+q)=
��2�������������ɣ�ֱ��д����ʽ�Ľ����(x-199)(x+201)=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ѧ�������Ķ���ϰ�ߣ���ѧУ�ձ鿪չ�ˡ��ҵ���.�й��Ρ������Ķ����ijУΪ�˽����꼶1200��ѧ���������Ķ�����ʱ������������������˲���ͬѧ�����������ͳ�ƣ����������Ƴ����²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ����������⣺
��1������ a= ��b= ��
��2���벹ȫƵ���ֲ�ֱ��ͼ�п�ȱ�IJ��֣�
��3�������У�ѧ�����Ķ�����ʱ�����λ�����ڵ� �飻
��4������Ƹ�У���꼶ѧ�����Ķ������� 1 Сʱ��������
��� | ʱ��Σ�Сʱ�� | Ƶ�� | Ƶ�� |
1 | 0��x��0.5 | 10 | 0.05 |
2 | 0.5��x��1.0 | 20 | 0.10 |
3 | 1.0��x��1.5 | 80 | b |
4 | 1.5��x��2.0 | a | 0.35 |
5 | 2.0��x��2.5 | 12 | 0.06 |
6 | 2.5��x��3.0 | 8 | 0.04 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
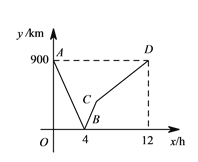
����Ŀ��һ�п쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ��������������ʻ��ʱ��Ϊ![]() ������֮��ľ���Ϊ
������֮��ľ���Ϊ![]() ��ͼ�е����߱�ʾ
��ͼ�е����߱�ʾ![]() ��
��![]() ֮��ĺ�����ϵ������ͼ�����һ��̽����
֮��ĺ�����ϵ������ͼ�����һ��̽����
��Ϣ��ȡ��1���ס�������֮��ľ���Ϊ______![]() ��
��
��2�������ͼ�е�![]() ��ʵ�����壺_______
��ʵ�����壺_______
ͼ�����⣨3���������Ϳ쳵���ٶȣ�
��4�����߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��������5�����ڶ��п쳵Ҳ�Ӽس���ʻ���ҵأ��ٶ����һ�п쳵��ͬ���ڵ�һ�п쳵����������![]() ���Ӻڶ��п쳵��������������ڶ��п쳵�ȵ�һ�п쳵����������Сʱ��
���Ӻڶ��п쳵��������������ڶ��п쳵�ȵ�һ�п쳵����������Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������9�֣���ͼ����OΪRt��ABCб��AB�ϵ�һ�㣬��OAΪ�뾶����O��BC���ڵ�D����AC���ڵ�E������AD��

��1����֤��ADƽ����BAC��
��2������BAC = 60����OA = 2������Ӱ���ֵ�������������![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
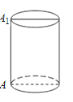
����Ŀ����ͼ����һľ��Բ����Ͳ�ĸ�Ϊ9cm������뾶Ϊ2cm,��ҪΧ�Ʊ�Ͳ�ı�����A��A1(A,A1��Բ����ͬһ�������)����һ����ɫ��������Ϊװ�Σ������������ߵ���̳�����_________cm.(��ȡ3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
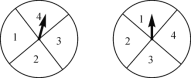
����Ŀ����ͼ������ת�̷ֱ�����ת��һ�Σ���ת��ֹͣת��ʱ������ָ��ֱ�����ij����������ʾ�����������������ĺ�Ϊ________�ĸ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��ֱ��y����![]() x��3��������ֱ��ڵ�A��B����ֱ��y��x���ڵ�C���߶�OA�ϵĵ�Q��ÿ��1����λ���ٶȴӵ�O�������A�������˶����˶�ʱ��Ϊt�룬����CQ.
x��3��������ֱ��ڵ�A��B����ֱ��y��x���ڵ�C���߶�OA�ϵĵ�Q��ÿ��1����λ���ٶȴӵ�O�������A�������˶����˶�ʱ��Ϊt�룬����CQ.
(1)�����C�����ꣻ
(2)����OQC�ǵ���ֱ�������Σ���t��ֵΪ________��
(3)��CQƽ����OAC���������ֱ��CQ��Ӧ�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�ߺ�Բ����һ���ǵ�����֪�ǵ�ʾ��ͼ����ͼ��ʾ����˵����A��O��B�䣽��AOB��������ȫ�������ε�_____��ȣ���ȫ�ȵ�������_____��
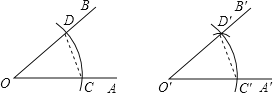
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com