
【题目】用直尺和圆规作一个角等于已知角的示意图,如图所示,则说明∠A′O′B′=∠AOB的依据是全等三角形的_____相等.其全等的依据是_____.
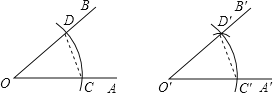
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
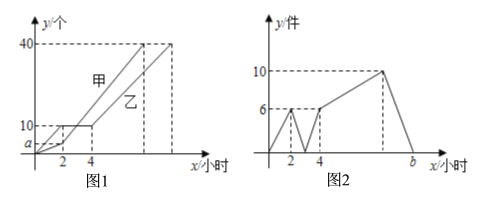
【题目】甲、乙两人分别安装同一种零件40个,其中乙在安装两小时后休息了2小时,后继续按原来进度工作,他们每人安装的零件总数y(个)与安装时间x(小时)的函数关系如图1所示,两人安装零件总数之差z(件)与时间x(小时)的函数关系如图2所示.
(1)a= ;b= .
(2)求出甲工作2小时后的安装的零件数y与时间x的函数关系.
(3)甲、乙两人在什么时间生产的零件总数相差8个?
查看答案和解析>>
科目:初中数学 来源: 题型:
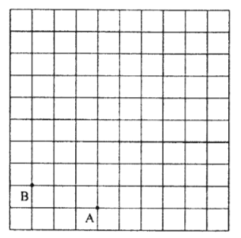
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点![]() 、点
、点![]() 在网格中的位置如图所示.
在网格中的位置如图所示.
(1)建立适当的平面直角坐标系,使点![]() 、点
、点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ;
;
(2)点![]() 的坐标为
的坐标为![]() ,在平面直角坐标系中标出点
,在平面直角坐标系中标出点![]() 的位置,连接
的位置,连接![]() 、
、![]() 、
、![]() ,
,
(3)若![]() 各项点的横坐标不变,纵坐标均乘以
各项点的横坐标不变,纵坐标均乘以![]() 在图中做出对应图形
在图中做出对应图形![]() ;
;
(4)![]() 与
与![]() 的位置关系为______;
的位置关系为______;![]() 的面积为______.
的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
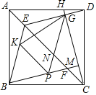
【题目】如图,四边形![]() 为正方形,
为正方形,![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在线段
,在线段![]() 上作
上作![]() ,连接
,连接![]() ,
,![]() ,其中
,其中![]() 交
交![]() 于
于![]() 点,
点,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PA+PB的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子与地面的夹角为45°:将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子与地面的夹角为75°,则小巷宽度w=( )
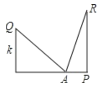
A.hB.kC.aD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
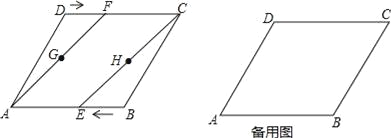
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com