
【题目】如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子与地面的夹角为45°:将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子与地面的夹角为75°,则小巷宽度w=( )
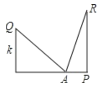
A.hB.kC.aD.![]()
【答案】A
【解析】
连接QR,过Q作QD⊥PR,则可证△AQR为等边三角形,得QR=AQ,进而求证△DQR≌△PRA,可得QD=RP,即墙面之间距离w=h.
解:连接QR,过Q作QD⊥PR,
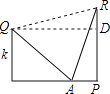
∵Q离开地面的高度为k,梯子与地面的夹角为45°;
∴∠AQD=45°,
又∵R点离开地面的高度为h,且此时梯子与地面的夹角为75°
∴∠QAR=180°-75°-45°=60°,且AQ=AR,
∴△AQR为等边三角形,
即AQ=QR=AR,
∵∠AQD=45°
∴∠RQD=60°-45°=15°
∠ARP=90°-∠RAP=90°-75°=15°,
∴∠RQD=∠ARP
又∵∠QDR=∠P=90°,AR=QR
∴△DQR≌△PRA,
∴QD=PR,即w=h.
故选:A.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图,如图所示,则说明∠A′O′B′=∠AOB的依据是全等三角形的_____相等.其全等的依据是_____.
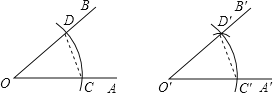
查看答案和解析>>
科目:初中数学 来源: 题型:
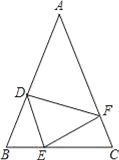
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购这两种原料的价格如下表:
甲 | 乙 | |
维生素C(单位/千克) | 600 | 100 |
原料价格(元/千克) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元.请问:既要符合要求又要成本最低,则购买甲种原料应该在什么范围之内,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)已知直线![]() 与抛物线
与抛物线![]() 相交于抛物线的顶点
相交于抛物线的顶点![]() 和另一点
和另一点![]() ,点
,点![]() 在第四象限.
在第四象限.
![]() 若点
若点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 过点
过点![]() 作
作![]() 轴的平行线与抛物线
轴的平行线与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com