
【题目】(题文)已知直线![]() 与抛物线
与抛物线![]() 相交于抛物线的顶点
相交于抛物线的顶点![]() 和另一点
和另一点![]() ,点
,点![]() 在第四象限.
在第四象限.
![]() 若点
若点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 过点
过点![]() 作
作![]() 轴的平行线与抛物线
轴的平行线与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
【答案】![]() 点
点![]() 坐标为
坐标为![]() .
.![]()
![]() .
.
【解析】
(1)由P点横坐标可求解b值,将P点代入抛物线可求解c值,从而求解Q点坐标;
(2)代入x=![]() 及
及![]() 可求解出
可求解出![]() ,由题意可知△QEP为直角等腰三角形,则M点坐标可表示为(0,-2
,由题意可知△QEP为直角等腰三角形,则M点坐标可表示为(0,-2![]() ),再利用M和P点坐标求解出直线解析式后联立二次函数解得
),再利用M和P点坐标求解出直线解析式后联立二次函数解得![]() ,运用三角形面积公式
,运用三角形面积公式![]() 可列出表达式进行求解.
可列出表达式进行求解.
![]() 由题意:
由题意:![]() ,
,
∴![]() ,∴抛物线为
,∴抛物线为![]() ,将
,将![]() 代入得到,
代入得到,![]() ,
,
∴![]() ,
,
∴抛物线解析式为![]() ,
,
∵点![]() 横坐标为
横坐标为![]() ,
,
∴点![]() 坐标为
坐标为![]() .
.
![]() 代入x=
代入x=![]() 及
及![]() ,则y=
,则y=![]() ,则
,则![]() ,
,
∵△QEP为直角等腰三角形,
∴yM+2=-![]() ,
,
∴M点坐标为(0,-2![]() ),
),
代入P和M点坐标,求解直线解析式:
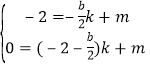 解得
解得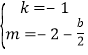 ,
,
∴直线![]() 为
为![]() ,
,
由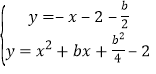 解得
解得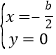 和
和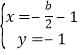 ,
,
∴点![]() 坐标
坐标![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 时,
时,![]() ,
,
根据函数的增减性可知,![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子与地面的夹角为45°:将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子与地面的夹角为75°,则小巷宽度w=( )
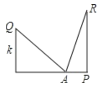
A.hB.kC.aD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
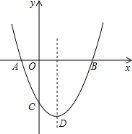
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,对称轴为直线
,对称轴为直线![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() ,下面五个结论:
,下面五个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④一元二次方程
;④一元二次方程![]() 必有两个不相等的实数根;⑤
必有两个不相等的实数根;⑤![]() .
.
那么,其中正确的结论是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发在线段
出发在线段![]() 移动,以
移动,以![]() 为腰作等腰
为腰作等腰![]() ,
,![]() ,连接
,连接![]() .
.
(1)如图,求证:![]() ≌
≌![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,试问:
,试问:![]() 的面积有没有最大值,如没有请说明理由,如有请求出最大值.
的面积有没有最大值,如没有请说明理由,如有请求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
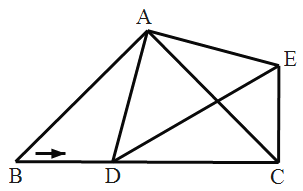
【题目】如图,在△ACD和△BCE中, AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
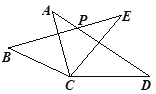
A.110°B.125°C.130°D.155°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(﹣3,0)、D(0,3),直线l1所对应的函数关系式为y=﹣2x﹣2.
(1)求点C的坐标及直线l2所对应的函数关系式;
(2)求△ABC的面积;
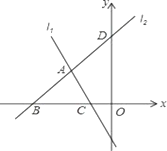
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com