
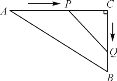
【题目】如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速移动,同时另一点Q从点C开始以3 cm/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300 cm2时,运动时间为__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
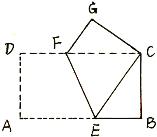
【题目】如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)试判断△CEF的形状,并证明你的结论;
(3)若AB=8,AD=4,求四边形ECGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
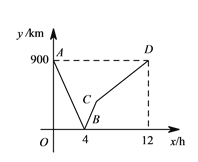
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系,根据图象进行一下探究:
之间的函数关系,根据图象进行一下探究:
信息读取(1)甲、乙两地之间的距离为______![]() :
:
(2)请解释图中点![]() 的实际意义:_______
的实际意义:_______
图象理解(3)求慢车和快车的速度:
(4)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围:
的取值范围:
问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇![]() 分钟后,第二列快车与慢车相遇,求第二列快车比第一列快车晚出发多少小时?
分钟后,第二列快车与慢车相遇,求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
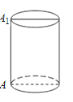
【题目】如图,有一木质圆柱笔筒的高为9cm,底面半径为2cm,现要围绕笔筒的表面由A到A1(A,A1在圆柱的同一轴截面上)镶上一条银色金属线作为装饰,则这条金属线的最短长度是_________cm.(π取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
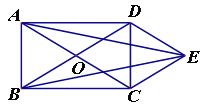
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,直线y=-![]() x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
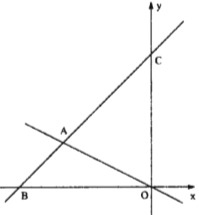
【题目】如图,平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
(1)求直线![]() 的表达式.
的表达式.
(2)求![]() 的面积.
的面积.
(3)直接写出使![]() 的面积是
的面积是![]() 面积的
面积的![]() 的点
的点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购这两种原料的价格如下表:
甲 | 乙 | |
维生素C(单位/千克) | 600 | 100 |
原料价格(元/千克) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元.请问:既要符合要求又要成本最低,则购买甲种原料应该在什么范围之内,最低成本是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com