
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
【答案】(1)见解析(2)成立
【解析】
试题(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.
(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可
得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
试题解析:(1)在正方形ABCD中,
∴△CBE≌△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°. CE=CF
∵∠GCE=∠GCF, GC=GC
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.


科目:初中数学 来源: 题型:
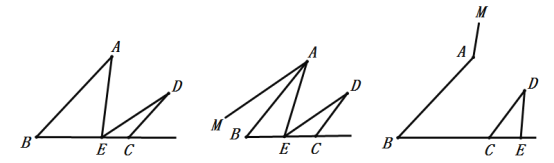
【题目】点D在∠ABC内,点E为边BC上一点,连接DE、CD.
(1)如图1,连接AE,若∠AED=∠A+∠D,求证:AB//CD.
(2)在(1)的结论下,过点A的直线MA//ED.
①如图2,当点E在线段BC上时,猜想并验证∠MAB与∠CDE的数量关系;
②如图3,当点E在线段BC的延长线上时,猜想并验证∠MAB与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆实验外国语学校是一所外语小班制教学的特色学校,初二年级某英语小班共有![]() 名同学,学号依次为
名同学,学号依次为![]() 号,
号,![]() 号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(
号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(![]() 号)调整到甲组,将丙组的小英(
号)调整到甲组,将丙组的小英(![]() 号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加
号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加![]() ,乙组同学学号的平均数将比调整前增加
,乙组同学学号的平均数将比调整前增加![]() ;同时乙组的小强(
;同时乙组的小强(![]() 号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题:
(1)初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?
(2)若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)
(3)如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,周长为a的圆上有且仅有一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过4个整数点(不包括A、B两点),则a的取值范围为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() 是
是![]() 上的点,
上的点, ![]() 相交于点
相交于点![]() .
.
(1) 如图2,若![]() =90°,求证:
=90°,求证: ![]()
![]() ;
;
(2) 如图1,若![]() =
=![]() ( 0°<
( 0°< ![]() <180°).
<180°).
①求![]()
![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②是否存在![]() ,使
,使![]() 小于
小于![]() ,如果存在,求出
,如果存在,求出![]() 的范围,如果不存在,请说明理由.
的范围,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com