
【题目】点D在∠ABC内,点E为边BC上一点,连接DE、CD.
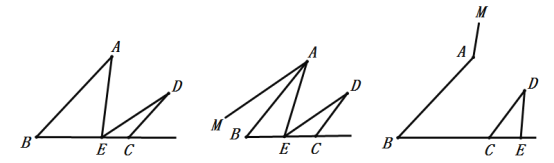
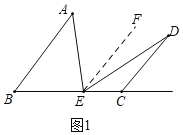
(1)如图1,连接AE,若∠AED=∠A+∠D,求证:AB//CD.
(2)在(1)的结论下,过点A的直线MA//ED.
①如图2,当点E在线段BC上时,猜想并验证∠MAB与∠CDE的数量关系;
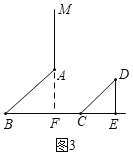
②如图3,当点E在线段BC的延长线上时,猜想并验证∠MAB与∠CDE的数量关系.
【答案】(1)证明见解析;(2)①∠MAB=∠CDE;②∠CDE+∠MAB=180°.
【解析】
(1)过E作EF∥AB,则∠A=∠AEF,由∠D=∠AED﹣∠A,∠DEF=∠AED﹣∠AEF,即可得到∠D=∠DEF,进而得出EF∥CD,即可得到AB∥CD;
(2)①根据∠AED=∠BAE+∠D,∠MAE=∠BAE+∠BAE,即可得到∠D=∠BAM,即可得到结论;
②延长MA交BC于F,依据平行线的性质以及三角形内角和定理,即可得到∠D=∠BAF,再根据邻补角互补即可得到∠CDE+∠MAB=180°.
(1)如图1,过E作EF∥AB,则∠A=∠AEF.
∵∠AED=∠A+∠D,∴∠D=∠AED﹣∠A.
又∵∠DEF=∠AED﹣∠AEF,∴∠D=∠DEF,∴EF∥CD,∴AB∥CD;
(2)①∵AM∥DE,∴∠MAE=∠AED.
∵∠AED=∠BAE+∠D,∠MAE=∠BAE+∠BAE,∴∠D=∠BAM,即∠MAB=∠CDE;
②如图3,延长MA交BC于F.
∵MA∥ED,∴∠DEC=∠MFB.
∵AB∥CD,∴∠B=∠DCE,∴∠D=∠BAF.
又∵∠BAF+∠MAB=180°,∴∠CDE+∠MAB=180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】历史上对勾股定理的一种证法采用了如图所示图形,其中两个全等的直角三角形边AE,EB在一条直线上.证明中用到的面积相等关系是 ( )
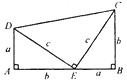
A. S△EDA=S△CEB
B. S△EDA +S△CEB=S△CDB
C. S四边形CDAE= S四边形CDEB
D. S△EDA+S△CDE+S△CEB= S四边形ABCD
查看答案和解析>>
科目:初中数学 来源: 题型:
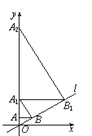
【题目】如图,直线l:y =![]() x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线![]() 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
A. (0,42019) B. (0,42018) C. (0,32019) D. (0,32018)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:(只填写序号).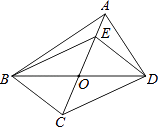
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究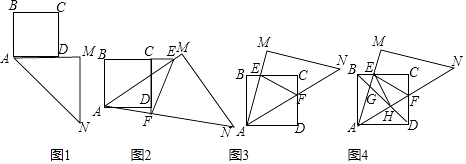
综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE﹣DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=度;
②猜想:线段EF,BE,DF三者之间的数量关系是: .
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com