练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】历史上对勾股定理的一种证法采用了如图所示图形，其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是 ( )

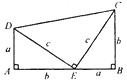
    A. S△EDA=S△CEB

    B. S△EDA +S△CEB=S△CDB

    C. S四边形CDAE= S四边形CDEB

    D. S△EDA+S△CDE+S△CEB= S四边形ABCD

    【答案】D

    【解析】

    用三角形的面积和、梯形的面积来表示这个图形的面积，从而证明勾股定理．

    ∵由S△EDA+S△CDE+S△CEB=S四边形ABCD．
    可知ab+c2+ab=（a+b）2，
    ∴c2+2ab=a2+2ab+b2，整理得a2+b2=c2，
    ∴证明中用到的面积相等关系是：S△EDA+S△CDE+S△CEB=S四边形ABCD．
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将三角形ABC向左平移至点B与原点重合，得三角形A′OC′．

    （1）直接写出三角形ABC的三个顶点的坐标A　　，B　　，C　　；

    （2）画出三角形A′OC′；

    （3）求三角形ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．

    （1）求购买一个甲种足球、一个乙种足球各需多少元？

    （2）为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个．恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    在解形如3|x-2|=|x-2|+4这一类含有绝对值的方程时，我们可以根据绝对值的意义分x＜2和x≥2两种情况讨论：

    ①当x＜2时，原方程可化为-3（x-2）=-（x-2）+4，解得：x=0，符合x＜2

    ②当x≥2时，原方程可化为3（x-2）=（x-2）+4，解得：x=4，符合x≥2

    ∴原方程的解为：x=0，x=4．

    解题回顾：本题中2为x-2的零点，它把数轴上的点所对应的数分成了x＜2和x≥2两部分，所以分x＜2和x≥2两种情况讨论．

    知识迁移：

    （1）运用整体思想先求|x-3|的值，再去绝对值符号的方法解方程：|x-3|+8=3|x-3|；

    知识应用：

    （2）运用分类讨论先去绝对值符号的方法解类似的方程：|2-x|-3|x+1|=x-9．

    （提示：本题中有两个零点，它们把数轴上的点所对应的数分成了几部分呢？）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

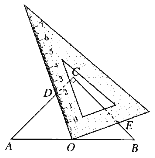
    【题目】如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，边AC的长为，将一块边长足够大的三角板的直角顶点放在点O处，将三角板绕点O旋转，始终保持三角板的一条直角边与 AC相交，交点为点D，另一条直角边与BC相交，交点为点E．证明：等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，动点P从点B出发，沿BC→CD→DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，y关于x的函数图象如图2所示，则m的值是（ ）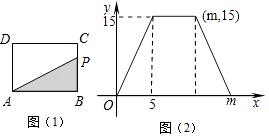

    A.6
    B.8
    C.11
    D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，点B，E分别在AC，DF上，BD，CE均与AF相交，∠1＝∠2，∠C＝∠D，求证：∠A＝∠F．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

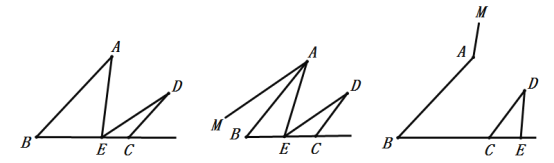
    【题目】点D在∠ABC内，点E为边BC上一点，连接DE、CD．

    （1）如图1，连接AE，若∠AED=∠A+∠D，求证：AB//CD．

    （2）在（1）的结论下，过点A的直线MA//ED．

    ①如图2，当点E在线段BC上时，猜想并验证∠MAB与∠CDE的数量关系；

    ②如图3，当点E在线段BC的延长线上时，猜想并验证∠MAB与∠CDE的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】规定两数a，b之间的一种运算，记作(a，b)：如果，那么(a，b)=c．

    例如：因为23=8，所以(2，8)=3．

    (1)根据上述规定，填空：

    （3，9）=_____，（5，125）=_____，（，）=_____，（-2，-32）=_____．

    (2)令，，，试说明下列等式成立的理由：.

    查看答案和解析>>

    同步练习册答案