
【题目】阅读理解:
在解形如3|x-2|=|x-2|+4这一类含有绝对值的方程时,我们可以根据绝对值的意义分x<2和x≥2两种情况讨论:
①当x<2时,原方程可化为-3(x-2)=-(x-2)+4,解得:x=0,符合x<2
②当x≥2时,原方程可化为3(x-2)=(x-2)+4,解得:x=4,符合x≥2
∴原方程的解为:x=0,x=4.
解题回顾:本题中2为x-2的零点,它把数轴上的点所对应的数分成了x<2和x≥2两部分,所以分x<2和x≥2两种情况讨论.
知识迁移:
(1)运用整体思想先求|x-3|的值,再去绝对值符号的方法解方程:|x-3|+8=3|x-3|;
知识应用:
(2)运用分类讨论先去绝对值符号的方法解类似的方程:|2-x|-3|x+1|=x-9.
(提示:本题中有两个零点,它们把数轴上的点所对应的数分成了几部分呢?)
【答案】(1)![]() ;(2)
;(2)![]() =-14或
=-14或![]() =
=![]() .
.
【解析】
(1)先把|x-3|-3|x-3|=-8看作是关于|x-3|的一元一次方程,可解得|x-3|=4,再去绝对值得到x-3=±4,然后解两个一元一次方程即可;
(2)2-x的零点为2,x+1的零点为-1,这样分三个区间进行讨论:当x≤-1;当-1<x≤2;当-1<x≤2;在各区间分别去绝对值化为一元一次方程,解方程,然后得到满足条件的x的值.
解:(1)移项得|x-3|-3|x-3|=-8,
合并得-2|x-3|=-8,
两边除以-2得|x-3|=4,
所以x-3=±4,
∴x=-1或7;
(2)当x≤-1,原方程可化为2-x+3(x+1)=x-9,解得x=-14,符合x≤-1;
当-1<x≤2,原方程可化为2-x-3(x+1)=x-9,解得x=![]() ,符合-1<x≤2;
,符合-1<x≤2;
当x>2,原方程可化为-2+x+3(x+1)=x-9,解得x=![]() ,不符合x>2;
,不符合x>2;
∴原方程的解为x=-14或x=![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如图所示的两幅不完整的统计图.(![]() 把圆分成面积相等的两部分)请根据图中提供的信息,解答下列问题:
把圆分成面积相等的两部分)请根据图中提供的信息,解答下列问题:
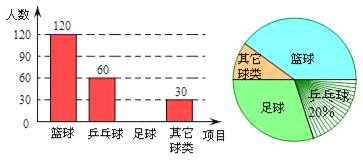
(1)参加调查的人数共有_______人;在扇形图中,表示“其它球类”的扇形的圆心角为______度;
(2)将条形图补充完整;
(3)若该校有![]() 名学生,估计喜欢“乒乓球”的学生共有多少人?
名学生,估计喜欢“乒乓球”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B和线段CD都在数轴上,点A、C、D、B起始位置所表示的数分别为-2、0、3、12;线段CD沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
(1)用含有t的代数式表示AC的长为多少,当t=2秒时,AC的长为多少.
(2)当0<t<9时AC+BD等于多少,当t>9时AC+BD等于多少.
(3)若点A与线段CD同时出发沿数轴的正方向移动,点A的速度为每秒2个单位,在移动过程中,是否存在某一时刻使得AC=2BD,若存在,请直接写出t的值;若不存在,请说明理由.
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】历史上对勾股定理的一种证法采用了如图所示图形,其中两个全等的直角三角形边AE,EB在一条直线上.证明中用到的面积相等关系是 ( )
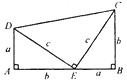
A. S△EDA=S△CEB
B. S△EDA +S△CEB=S△CDB
C. S四边形CDAE= S四边形CDEB
D. S△EDA+S△CDE+S△CEB= S四边形ABCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y =![]() x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线![]() 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
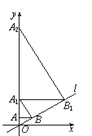
A. (0,42019) B. (0,42018) C. (0,32019) D. (0,32018)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究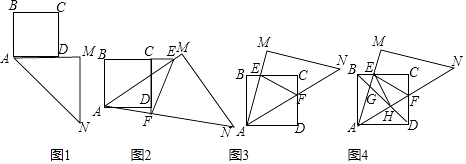
综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE﹣DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=度;
②猜想:线段EF,BE,DF三者之间的数量关系是: .
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com