练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线l：y =x，过点A（0，1）作y轴的垂线交直线于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…按此作法继续下去，则点A2019的坐标为( )

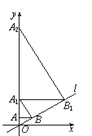
    A. （0，42019） B. （0，42018） C. （0，32019） D. （0，32018）

    【答案】A

    【解析】

    根据所给直线解析式可得直线l与x轴的夹角，进而根据所给条件依次得到点A1，A2的坐标，通过相应规律得到A2019的坐标即可．

    ∵直线l的解析式为：y=x，

    ∴直线l与x轴的夹角为30，

    ∵AB∥x轴，

    ∴∠ABO=30，

    ∵OA=1，

    ∴AB=，

    ∵A1B⊥直线l，

    ∴∠AB A1=60，

    ∴A A1=3，

    ∴A1 (0,4)，

    同理可得A2 (0,16)，

    …，

    ∴A2019纵坐标为：，

    ∴A2019 (0).

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将 沿CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC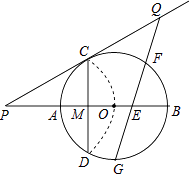

    （1）求CD的长；
    （2）求证：PC是⊙O的切线；
    （3）点G为 的中点，在PC延长线上有一动点Q，连接QG交AB于点E．交 于点F（F与B、C不重合）．问GEGF是否为定值？如果是，求出该定值；如果不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    在解形如3|x-2|=|x-2|+4这一类含有绝对值的方程时，我们可以根据绝对值的意义分x＜2和x≥2两种情况讨论：

    ①当x＜2时，原方程可化为-3（x-2）=-（x-2）+4，解得：x=0，符合x＜2

    ②当x≥2时，原方程可化为3（x-2）=（x-2）+4，解得：x=4，符合x≥2

    ∴原方程的解为：x=0，x=4．

    解题回顾：本题中2为x-2的零点，它把数轴上的点所对应的数分成了x＜2和x≥2两部分，所以分x＜2和x≥2两种情况讨论．

    知识迁移：

    （1）运用整体思想先求|x-3|的值，再去绝对值符号的方法解方程：|x-3|+8=3|x-3|；

    知识应用：

    （2）运用分类讨论先去绝对值符号的方法解类似的方程：|2-x|-3|x+1|=x-9．

    （提示：本题中有两个零点，它们把数轴上的点所对应的数分成了几部分呢？）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，动点P从点B出发，沿BC→CD→DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，y关于x的函数图象如图2所示，则m的值是（ ）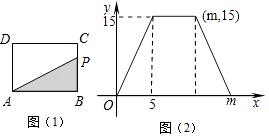

    A.6
    B.8
    C.11
    D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，点B，E分别在AC，DF上，BD，CE均与AF相交，∠1＝∠2，∠C＝∠D，求证：∠A＝∠F．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1为深50cm的圆柱形容器，底部放入一个长方体的铁块，现在以一定的速度向容器内注水，图2为容器顶部离水面的距离y（cm）随时间t（分钟）的变化图象，则（ ）

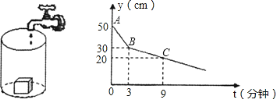
    A. 注水的速度为每分钟注入cm高水位的水

    B. 放人的长方体的高度为30cm

    C. 该容器注满水所用的时间为21分钟

    D. 此长方体的体积为此容器的体积的0.35.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

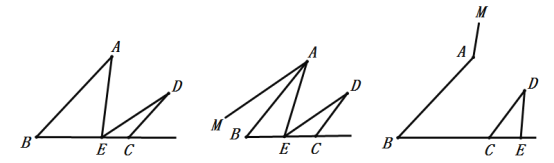
    【题目】点D在∠ABC内，点E为边BC上一点，连接DE、CD．

    （1）如图1，连接AE，若∠AED=∠A+∠D，求证：AB//CD．

    （2）在（1）的结论下，过点A的直线MA//ED．

    ①如图2，当点E在线段BC上时，猜想并验证∠MAB与∠CDE的数量关系；

    ②如图3，当点E在线段BC的延长线上时，猜想并验证∠MAB与∠CDE的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y1=kx+2与反比例函数y2= 的图象交于点A（m，3），与坐标轴分别交于B，C两点．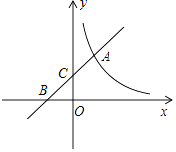

    （1）若y1＞y2＞0，求自变量x的取值范围；
    （2）动点P（n，0）在x轴上运动，当n为何值时，|PA﹣PC|的值最大？并求最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算
    （1）计算：（3﹣π）0+4sin45°﹣ +|1﹣ |
    （2）化简求值：（ + ）÷ ，其中x=6．

    查看答案和解析>>

    同步练习册答案