
【题目】计算
(1)计算:(3﹣π)0+4sin45°﹣ ![]() +|1﹣
+|1﹣ ![]() |
|
(2)化简求值:( ![]() +
+ ![]() )÷
)÷ ![]() ,其中x=6.
,其中x=6.
【答案】
(1)解:原式=1+4﹣2 ![]() +
+ ![]() ﹣1
﹣1
=4﹣2 ![]() +
+ ![]()
(2)解:当x=6时,
∴原式=( ![]() ﹣
﹣ ![]() )×
)× ![]()
= ![]() ﹣
﹣ ![]()
= ![]()
=﹣ ![]()
【解析】(1)根据任何一个不等于零的数的零次幂都等于1;原式=1+4﹣2![]() +
+![]() ﹣1=4﹣2
﹣1=4﹣2![]() +
+ ![]() ;(2)先把原分式的分子分母分解因式,化简为最简分式;当x=6时,原式=
;(2)先把原分式的分子分母分解因式,化简为最简分式;当x=6时,原式=![]() =-
=-![]() .
.
【考点精析】根据题目的已知条件,利用零指数幂法则和特殊角的三角函数值的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


科目:初中数学 来源: 题型:
【题目】如图,直线l:y =![]() x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线![]() 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
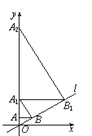
A. (0,42019) B. (0,42018) C. (0,32019) D. (0,32018)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究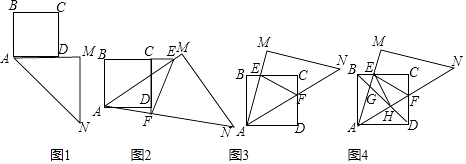
综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE﹣DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=度;
②猜想:线段EF,BE,DF三者之间的数量关系是: .
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
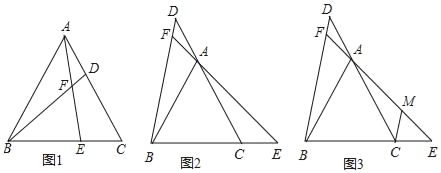
【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现![]() 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润![]() 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高![]() ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?
(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地 | |
一次性购买的数量 | 折扣数 |
不超过150盏的部分 |
|
超过150盏的部分 | 9折 |
表二
乙生产基地 | |
出厂总金额 | 返现金 |
不超过5640元 | 0元 |
超过5640元,但不超过9353元 | 返现300元 |
超过9353元 | 先返现出厂总金额的 |
已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1 =∠2,∠BAC = 75°将求∠AGD的过程填写完整
解:∵EF∥AD
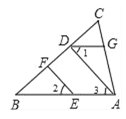
∴ ∠2 = ( )
又∵ ∠1 = ∠2
∴ ∠1 = ∠3。( )
∴AB∥ 。( )
∴∠BAC + = 180°。( )
∵∠BAC=75°∴∠AGD = 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
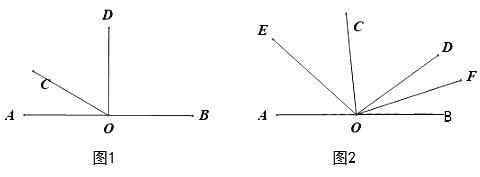
【题目】如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数;
(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD,多少秒时∠COM=∠BON(直接写出答案,不必写出过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com