
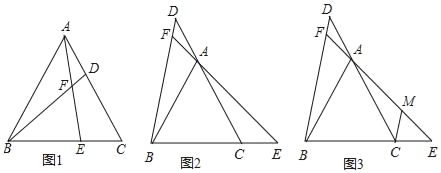
【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
【答案】(1)证明见解析;(2)60°;(3)6.
【解析】
(1)先判断出∠BAC=∠ACB,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(2)先判断出∠BAD=∠ACE=120°,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(3)先求出AC=12,再判断出△ADF∽△ACM,即可得出结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
在△ABD和△CAE中,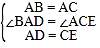 ,
,
∴△ABD≌△CAE,
∴BD=AE,
(2)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
∴∠BAD=∠ACE=120°
在△ABD和△CAE中,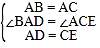 ,
,
∴△ABD≌△CAE,
∴∠ADB=∠CEA,
∴∠BFE=∠ADB+∠DAF=∠AEC+∠CAE=∠ACB=60°;
(3)∵CM∥BD,
∴△ADF∽△ACM,
∴![]() ,
,
∵AF:AM=2:4=1:2,
∴AD=![]() AC,
AC,
∵△ABC是等边三角形,
∴AC=BC=12,
∴AD=6,
∵AD=CE,
∴CE=AD=6.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC→CD→DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,则m的值是( )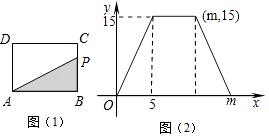
A.6
B.8
C.11
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=kx+2与反比例函数y2= ![]() 的图象交于点A(m,3),与坐标轴分别交于B,C两点.
的图象交于点A(m,3),与坐标轴分别交于B,C两点.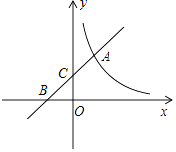
(1)若y1>y2>0,求自变量x的取值范围;
(2)动点P(n,0)在x轴上运动,当n为何值时,|PA﹣PC|的值最大?并求最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )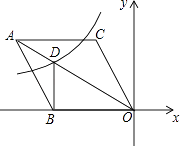
A.6 ![]()
B.﹣6 ![]()
C.12 ![]()
D.﹣12 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]() ,
,![]() 那么(a,b)=c.
那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,9)=_____,(5,125)=_____,(![]() ,
,![]() )=_____,(-2,-32)=_____.
)=_____,(-2,-32)=_____.
(2)令![]() ,
,![]() ,
,![]() ,试说明下列等式成立的理由:
,试说明下列等式成立的理由:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
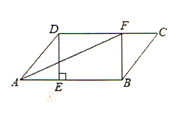
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com