练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图1，在矩形ABCD中，动点P从点B出发，沿BC→CD→DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，y关于x的函数图象如图2所示，则m的值是（ ）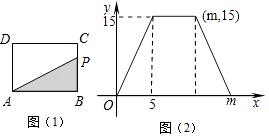

    A.6
    B.8
    C.11
    D.16

    【答案】C
    【解析】解：动点P从点B出发，沿BC、CD、DA运动至点A停止，

    ∵当点P运动到点C，D之间时，△ABP的面积不变．函数图象上横轴表示点P运动的路程，

    ∴x=5时，y开始不变，说明BC=5，

    ∴△ABC的面积为：y= ×AB×5=15．

    ∴AB=6，

    ∵四边形ABCD为矩形，

    ∴CD=AB=6，

    ∴M=5+6=11．

    所以答案是：C．

    【考点精析】掌握矩形的性质是解答本题的根本，需要知道矩形的四个角都是直角，矩形的对角线相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，点的坐标为，将点向右平移个单位得到点，其中关于的一元一次不等式的解集为，过点作轴于得到长方形，

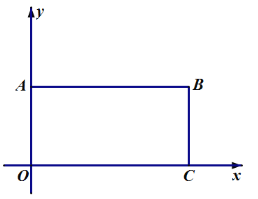
    （1）求点坐标______及四边形的面积_______；

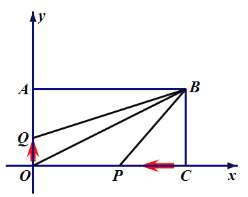
    （2）如图2，点从点以每秒个单位长度的速度在轴上向上运动，同时点从点以每秒个单位长度的速度匀速在轴上向左运动，设运动的时间为秒，问是否存在一段时间，使得的面积不大于的面积，若存在，求出的取值范围；若不存在，说明理由；

    （3）在（2）的条件下，四边形的面积是否发生变化，若不变化，请求出其值；若变化，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列结沦中，错误的有（　　）

    ①Rt△ABC中，已知两边分别为3和4，则第三边的长为5；②三角形的三边分别为a、b、c，若a2+b2=c2，则∠A=90°；③若△ABC中，∠A：∠B：∠C=1：5：6，则这个三角形是一个直角三角形；④若（x﹣y）2+M=（x+y）2成立，则M=4xy．

    A. 0个 B. 1个 C. 2个 D. 3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A、B和线段CD都在数轴上，点A、C、D、B起始位置所表示的数分别为-2、0、3、12；线段CD沿数轴的正方向以每秒1个单位的速度移动，移动时间为t秒．

    （1）用含有t的代数式表示AC的长为多少，当t=2秒时，AC的长为多少．

    （2）当0＜t＜9时AC+BD等于多少，当t＞9时AC+BD等于多少.

    （3）若点A与线段CD同时出发沿数轴的正方向移动，点A的速度为每秒2个单位，在移动过程中，是否存在某一时刻使得AC=2BD，若存在，请直接写出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】历史上对勾股定理的一种证法采用了如图所示图形，其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是 ( )

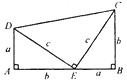
    A. S△EDA=S△CEB

    B. S△EDA +S△CEB=S△CDB

    C. S四边形CDAE= S四边形CDEB

    D. S△EDA+S△CDE+S△CEB= S四边形ABCD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级（1）班体育委员统计了全班同学60秒跳绳次数，并列出了下面的不完整频数分布表和不完整的频数分布直方图．根据图表中的信息解答问题

    组别

    跳绳次数

    频数

    A

    60≤x＜80

    2

    B

    80≤x＜100

    6

    C

    100≤x＜120

    18

    D

    120≤x＜140

    12

    E

    140≤x＜160

    a

    F

    160≤x＜180

    3

    G

    180≤x＜200

    1

    合计

    50

    （1）求a的值；

    （2）求跳绳次数x在120≤x＜180范围内的学生的人数；

    （3）补全频数分布直方图，并指出组距与组数分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l：y =x，过点A（0，1）作y轴的垂线交直线于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…按此作法继续下去，则点A2019的坐标为( )

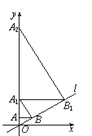
    A. （0，42019） B. （0，42018） C. （0，32019） D. （0，32018）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，对角线AC，BD相交于点O，且OB=OD．点E在线段OA上，连结BE，DE．给出下列条件：①OC=OE；②AB=AD；③BC⊥CD；④∠CBD=∠EBD．请你从中选择两个条件，使四边形BCDE是菱形，并给予证明．你选择的条件是：（只填写序号）．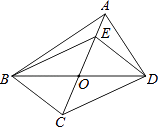

    查看答案和解析>>

    科目：初中数学 来源： 题型：

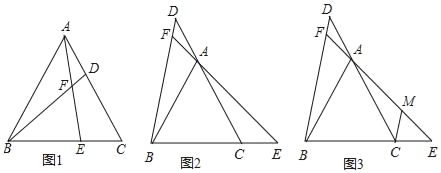
    【题目】已知△ABC是等边三角形，在直线AC、直线BC上分别取点D和点且AD=CE，直线BD、AE相交于点F．

    （1）如图1所示，当点D、点E分别在线段CA、BC上时，求证：BD=AE；

    （2）如图2所示，当点D、点E分别在CA、BC的延长线时，求∠BFE的度数；

    （3）如图3所示，在（2）的条件下，过点C作CM∥BD，交EF于点M，若DF：AF：AM=1：2：4，BC=12，求CE的长度．

    查看答案和解析>>

    同步练习册答案