
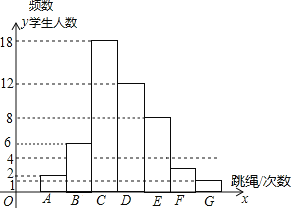
ЁОЬтФПЁПФГаЃЦпФъМЖЃЈ1ЃЉАрЬхг§ЮЏдБЭГМЦСЫШЋАрЭЌбЇ60УыЬјЩўДЮЪ§ЃЌВЂСаГіСЫЯТУцЕФВЛЭъећЦЕЪ§ЗжВМБэКЭВЛЭъећЕФЦЕЪ§ЗжВМжБЗНЭМЃЎИљОнЭМБэжаЕФаХЯЂНтД№ЮЪЬт
зщБ№ | ЬјЩўДЮЪ§ | ЦЕЪ§ |
A | 60ЁмxЃМ80 | 2 |
B | 80ЁмxЃМ100 | 6 |
C | 100ЁмxЃМ120 | 18 |
D | 120ЁмxЃМ140 | 12 |
E | 140ЁмxЃМ160 | a |
F | 160ЁмxЃМ180 | 3 |
G | 180ЁмxЃМ200 | 1 |
КЯМЦ | 50 | |
ЃЈ1ЃЉЧѓaЕФжЕЃЛ
ЃЈ2ЃЉЧѓЬјЩўДЮЪ§xдк120ЁмxЃМ180ЗЖЮЇФкЕФбЇЩњЕФШЫЪ§ЃЛ
ЃЈ3ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЌВЂжИГізщОргызщЪ§ЗжБ№ЪЧЖрЩйЃП

ЁОД№АИЁПЃЈ1ЃЉ8ЃЛЃЈ2ЃЉ23ШЫЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉгУ50МѕШЅAЁЂBЁЂCЁЂDЁЂFЁЂGзщЕФЦЕЪ§МДПЩЧѓЕУaЕФжЕЃЛ
ЃЈ2ЃЉНЋDЁЂEЁЂFШ§зщЕФЦЕЪ§ЯрМгМДПЩЕУЃЛ
ЃЈ3ЃЉИљОнaЕФжЕПЩВЙШЋжБЗНЭМЃЌИљОнЦЕЪ§ЗжВМБэМДПЩаДГізщОргызщЪ§.
ЃЈ1ЃЉa=50-ЃЈ2+6+18+12+3+1ЃЉ=8ЃЛ
ЃЈ2ЃЉЬјЩўДЮЪ§xдк120ЁмxЃМ180ЗЖЮЇФкЕФбЇЩњЕФШЫЪ§ЮЊ12+8+3=23ШЫЃЛ
ЃЈ3ЃЉВЙШЋЭМаЮШчЯТЃК
зщОрЮЊ20ЁЂзщЪ§ЮЊ7ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌAB=4ЃЌEЮЊBCЕФжаЕуЃЌFЮЊAEЕФжаЕуЃЌЙ§ЕуFзїGHЁЭAEЃЌЗжБ№НЛABКЭCDгкGЃЌHЃЌЧѓGFЕФГЄЃЌВЂЧѓ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛИіГЄЗНаЮдЫЖЏГЁБЛЗжИєГЩAЃЌBЃЌAЃЌBЃЌCЙВ5ИіЧјЃЌAЧјЪЧБпГЄЮЊa mЕФе§ЗНаЮЃЌCЧјЪЧБпГЄЮЊc mЕФе§ЗНаЮЃЎ
(1)СаЪНБэЪОУПИіBЧјГЄЗНаЮГЁЕиЕФжмГЄЃЌВЂНЋЪНзгЛЏМђЃЛ
(2)СаЪНБэЪОећИіГЄЗНаЮдЫЖЏГЁЕФжмГЄЃЌВЂНЋЪНзгЛЏМђЃЛ
(3)ШчЙћaЃН40ЃЌcЃН10ЃЌЧѓећИіГЄЗНаЮдЫЖЏГЁЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕБЉ1ЁмxЁм1ЪБЃЌЖўДЮКЏЪ§y=ЉЃЈxЉmЃЉ2+m2+1газюДѓжЕ4ЃЌдђЪЕЪ§mЕФжЕЮЊ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЙХДњЖдЙДЙЩЖЈРэгаЩюПЬЕФШЯЪЖЃЎ
(1)Ш§ЙњЪБДњЮтЙњЪ§бЇМведЫЌЕквЛДЮЖдЙДЙЩЖЈРэМгвджЄУїЃКгУЫФИіШЋЕШЕФЭМ1ЫљЪОЕФжБНЧШ§НЧаЮЦДГЩвЛИіЭМ2ЫљЪОЕФДѓе§ЗНаЮЃЌжаМфПеАзВПЗжЪЧвЛИіаЁе§ЗНаЮЃЎШчЙћДѓе§ЗНаЮЕФУцЛ§ЪЧ13ЃЌаЁе§ЗНаЮЕФУцЛ§ЪЧ1ЃЌжБНЧШ§НЧаЮЕФСНжБНЧБпЗжБ№ЮЊaЃЌbЃЌЧѓ(aЃЋb)2ЕФжЕЃЛ
(2)ЧхГЏЕФПЕЮѕЛЪЕлЖдЙДЙЩЖЈРэвВКмгабаОПЃЌЫћжјгаЁЖЛ§ЧѓЙДЙЩЗЈЁЗЃКгУЯжДњЕФЪ§бЇгябдУшЪіОЭЪЧЃКШєжБНЧШ§НЧаЮЕФШ§БпГЄЗжБ№ЮЊ3ЃЌ4ЃЌ5ЕФећЪ§БЖЃЌЩшЦфУцЛ§ЮЊSЃЌдђЧѓЦфБпГЄЕФЗНЗЈЮЊЃКЕквЛВН![]() ЃНmЃЛЕкЖўВНЃК
ЃНmЃЛЕкЖўВНЃК ![]() ЃНkЃЛЕкШ§ВНЃКЗжБ№гУ3ЃЌ4ЃЌ5ГЫkЃЌЕУШ§БпГЄЃЎЕБУцЛ§SЕШгк150ЪБЃЌЧыгУЁАЛ§ЧѓЙДЙЩЗЈЁБЧѓГіетИіжБНЧШ§НЧаЮЕФШ§БпГЄЃЎ
ЃНkЃЛЕкШ§ВНЃКЗжБ№гУ3ЃЌ4ЃЌ5ГЫkЃЌЕУШ§БпГЄЃЎЕБУцЛ§SЕШгк150ЪБЃЌЧыгУЁАЛ§ЧѓЙДЙЩЗЈЁБЧѓГіетИіжБНЧШ§НЧаЮЕФШ§БпГЄЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§y=ax2+bx+cЭМЯѓЕФвЛВПЗжЃЌЦфЖдГЦжсЮЊx=Љ1ЃЌЧвЙ§ЕуЃЈЉ3ЃЌ0ЃЉЯТСаЫЕЗЈЃК
ЂйabcЃМ0ЃЛЂк2aЉb=0ЃЛЂл4a+2b+cЃМ0ЃЛЂмШєЃЈЉ5ЃЌy1ЃЉЃЌЃЈ2ЃЌy2ЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1ЃОy2 ЃЎ
ЦфжаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ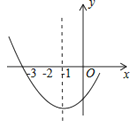
A.ЂйЂк
B.ЂкЂл
C.ЂкЂлЂм
D.ЂйЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
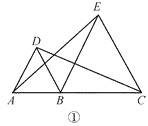
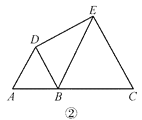
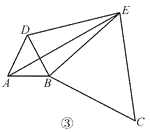
ЁОЬтФПЁПдкжБЯпЩЯЫГДЮШЁ AЃЌBЃЌC Ш§ЕуЃЌЗжБ№вд ABЃЌBC ЮЊБпГЄдкжБЯпЕФЭЌВрзїе§Ш§НЧаЮЃЌ зїЕУСНИіе§Ш§НЧаЮЕФСэвЛЖЅЕуЗжБ№ЮЊ DЃЌEЃЎ
(1)ШчЭМЂйЃЌСЌНс CDЃЌAEЃЌЧѓжЄЃКCDЃНAEЃЛ
(2)ШчЭМЂкЃЌШє ABЃН1ЃЌBCЃН2ЃЌЧѓ DE ЕФГЄЃЛ
(3)ШчЭМЂлЃЌНЋЭМЂкжаЕФе§Ш§НЧаЮ BCE ШЦ B ЕузїЪЪЕБЕФа§зЊЃЌСЌНс AEЃЌШєга DE2ЃЋBE2ЃН AE2ЃЌЪдЧѓЁЯDEB ЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
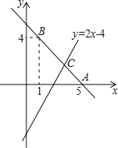
ЁОЬтФПЁПвбжЊжБЯпy=kx+bОЙ§ЕуAЃЈ5ЃЌ0ЃЉЃЌBЃЈ1ЃЌ4ЃЉЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєжБЯпy=2xЉ4гыжБЯпABЯрНЛгкЕуCЃЌЧѓЕуCЕФзјБъЃЛ
ЃЈ3ЃЉИљОнЭМЯѓЃЌаДГіЙигкxЕФВЛЕШЪН2xЉ4ЃОkx+bЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌAD=CDЃЌЁЯDAB=ЁЯACB=90ЁуЃЌЙ§ЕуDзїDEЁЭACЃЌДЙзуЮЊFЃЌDEгыABЯрНЛгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКABAF=CBCDЃЛ
ЃЈ2ЃЉвбжЊAB=15cmЃЌBC=9cmЃЌPЪЧЯпЖЮDEЩЯЕФЖЏЕуЃЎЩшDP=x cmЃЌЬнаЮBCDPЕФУцЛ§ЮЊycm2 ЃЎ
ЂйЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЎ
ЂкyЪЧЗёДцдкзюДѓжЕЃПШєгаЧѓГіетИізюДѓжЕЃЌШєВЛДцдкЧыЫЕУїРэгЩЃЎ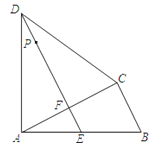
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com