
【题目】如图1,点![]() 的坐标为
的坐标为![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位得到点
个单位得到点![]() ,其中关于
,其中关于![]() 的一元一次不等式
的一元一次不等式![]() 的解集为
的解集为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() 得到长方形
得到长方形![]() ,
,
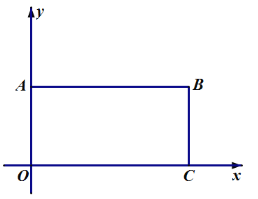
(1)求![]() 点坐标______及四边形
点坐标______及四边形![]() 的面积_______;
的面积_______;
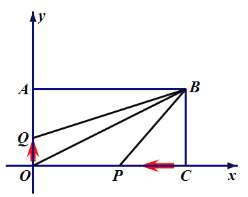
(2)如图2,点![]() 从
从![]() 点以每秒
点以每秒![]() 个单位长度的速度在
个单位长度的速度在![]() 轴上向上运动,同时点
轴上向上运动,同时点![]() 从
从![]() 点以每秒
点以每秒![]() 个单位长度的速度匀速在
个单位长度的速度匀速在![]() 轴上向左运动,设运动的时间为
轴上向左运动,设运动的时间为![]() 秒
秒![]() ,问是否存在一段时间,使得
,问是否存在一段时间,使得![]() 的面积不大于
的面积不大于![]() 的面积,若存在,求出
的面积,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)在(2)的条件下,四边形![]() 的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
【答案】(1)![]() ;
;![]() ;(2)存在,
;(2)存在,![]() ;(3)不变;值为
;(3)不变;值为![]() .
.
【解析】
(1)利用不等式求出m的值,结合平移的性质得出B、C点坐标,再利用矩形面积求法得出答案;
(2)利用Q,P点移动速度分别表示出△BOQ和△BOP的面积,进而得出t的取值范围,即可得出答案;
(3)利用![]()
(1)由![]() 得,
得,![]()
∵不等式![]() 的解集为
的解集为![]()
∴![]()
解得m= 4
∵点A的坐标为(0, 2), 且向右平移b个单位得到点B
∴B(4, 2)
∵BC⊥x轴于C
∴C(4,0)
∵AB//OC,∠AOC=∠BCO = 90°
∴∠B+∠OCB = 180°
∴∠B=90°
∴四边形AOCB是矩形
∴![]()
故答案为:![]() ;
;![]() ;
;
(2)存在,理由如下:
由题意知: OQ= t,CP= 2t
∵四边形AOCB是矩形,OC= 4
∴∠BAO=∠BCO= 90°,OP=4- 2t
∴AB⊥OA,BC⊥OC
∵ ![]()
若![]() 的面积不大于
的面积不大于![]() 的面积.则
的面积.则![]()
解得:![]()
∵t>0
∴![]()
(3)不变,理由如下:
∵![]()
∴![]()
= 2t+4- 2t
=4


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
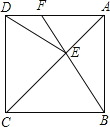
【题目】如图,在一方形ABCD中.E为对角线AC上一点,连接EB、ED,
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
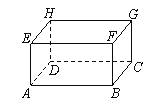
【题目】现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).
(1) 求线段BG的长;
(2) 现在箱外的点A处有一只蜘蛛,箱内的点C处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.(木板的厚度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将三角形ABC向左平移至点B与原点重合,得三角形A′OC′.
(1)直接写出三角形ABC的三个顶点的坐标A ,B ,C ;
(2)画出三角形A′OC′;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
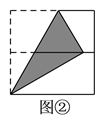
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC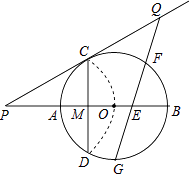
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC= ![]() ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )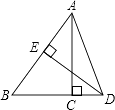
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC→CD→DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,则m的值是( )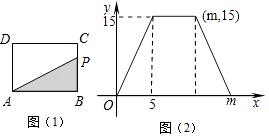
A.6
B.8
C.11
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com