[题目]规定两数a.b之间的一种运算.记作(a.b):如果.那么(a.b)=c．例如:因为23=8.所以(2.8)=3．(1)根据上述规定.填空:(3.9)= .(5.125)= .(.)= .(-2.-32)= ．(2)令...试说明下列等式成立的理由:. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】规定两数a，b之间的一种运算，记作(a，b)：如果，那么(a，b)=c．

例如：因为23=8，所以(2，8)=3．

(1)根据上述规定，填空：

（3，9）=_____，（5，125）=_____，（，）=_____，（-2，-32）=_____．

(2)令，，，试说明下列等式成立的理由：.

【答案】（1）2，3，4，5（2）

【解析】

（1）根据规定的运算法则计算即可；（2）令，，，根据规定的运算法则及同底数幂乘法的运算法则即可证明a+b=c，即可得结论.

（1）∵32=9，53=125，(-)4=，(-2)5=-32，

∴（3，9）=2，（5，125）=3，（，）=4，（-2，-32）=5.

故答案为：2；3；4；5

(2)令，，，则，，，

∵，

∴，

∴.

练习册系列答案

Happy寒假作业快乐寒假系列答案

金象教育U计划学期系统复习寒假作业系列答案

八斗才火线计划寒假西安交通大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】历史上对勾股定理的一种证法采用了如图所示图形，其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是 ( )

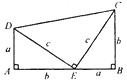
A. S△EDA=S△CEB

B. S△EDA +S△CEB=S△CDB

C. S四边形CDAE= S四边形CDEB

D. S△EDA+S△CDE+S△CEB= S四边形ABCD

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】平行四边形ABCD中，对角线AC、BD交于点O（如图），则图中全等三角形的对数为（　　）

A. 2 B. 3 C. 4 D. 5

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】操作与探究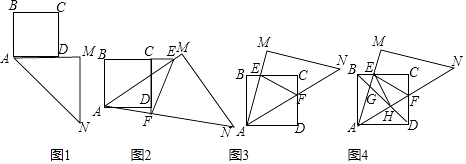

综合实践课，老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧，使边AM与AD在同
一直线上（如图1），其中∠AMN=90°，AM=MN．
（1）猜想发现
老师将三角尺AMN绕点A逆时针旋转α．如图2，当0＜α＜45°时，边AM，AN分别与直线BC，CD交于点E，F，连结EF．小明同学探究发现，线段EF，BE，DF满足EF=BE﹣DF；如图3，当45°＜α＜90°时，其它条件不变．
①填空：∠DAF+∠BAE=度；
②猜想：线段EF，BE，DF三者之间的数量关系是：．
（2）证明你的猜想；
（3）拓展探究
在45°＜α＜90°的情形下，连结BD，分别交AM，AN于点G，H，如图4连结EH，试证明：EH⊥AN．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）如图1，点P是平行四边形ABCD对角线AC、BD的交点，若S△PAB=S1，S△PBC=S2，S△PCD=S3，S△PAD=S4则S1、S2、S3、S4的关系为S1=S2=S3=S4．请你说明理由；

（2）变式1：如图2，点P是平行四边形ABCD内一点，连接PA、PB、PC、PD．若S△PAB=S1，S△PBC=S2，S△PCD=S3，S△PAD=S4，写出S1、S2、S3、S4的关系式；

（3）变式2：如图3，点P是四边形ABCD对角线AC、BD的交点若S△PAB=S1，S△PBC=S2，S△PCD=S3，S△PAD=S4，写出S1、S2、S3、S4的关系式．请你说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

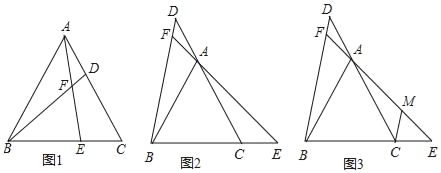
【题目】已知△ABC是等边三角形，在直线AC、直线BC上分别取点D和点且AD=CE，直线BD、AE相交于点F．

（1）如图1所示，当点D、点E分别在线段CA、BC上时，求证：BD=AE；

（2）如图2所示，当点D、点E分别在CA、BC的延长线时，求∠BFE的度数；

（3）如图3所示，在（2）的条件下，过点C作CM∥BD，交EF于点M，若DF：AF：AM=1：2：4，BC=12，求CE的长度．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏，A型日光灯每盏进价为40元，售价为60元，B型日光灯每盏进价为50元，售价为80元．

（1）求10月份两种新型节能日光灯各购进多少盏？

（2）将10月份购买的日光灯从生产基地运往商场的过程中，A型日光灯出现的损坏，B型日光灯完好无损，商场决定对A、B两种日光灯的售价进行调整，使这批日光灯全部售完后，商场可获得10664元的利润型日光灯在原售价基础上提高，问A型日光灯调整后的售价为多少元？

（3）进入11月份，B型日光灯的需求量增大，于是商场在筹备“双十一”促销活动时，决定去甲、乙两个生产基地只购进一批B型日光灯，甲、乙生产基地给出了不同的优惠措施：

甲生产基地：B型日光灯出厂价为每盏50元，折扣如表一所示

乙生产基地：B型日光灯出厂价为每盏47元，同时当出厂总金额达一定数量后还可按表二返现金．

表一

甲生产基地
一次性购买的数量	折扣数
不超过150盏的部分	折
超过150盏的部分	9折

表二

乙生产基地
出厂总金额	返现金
不超过5640元	0元
超过5640元，但不超过9353元	返现300元
超过9353元	先返现出厂总金额的后，再返现206元