
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
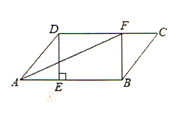
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
科目:初中数学 来源: 题型:
【题目】某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 | 跳绳次数 | 频数 |
A | 60≤x<80 | 2 |
B | 80≤x<100 | 6 |
C | 100≤x<120 | 18 |
D | 120≤x<140 | 12 |
E | 140≤x<160 | a |
F | 160≤x<180 | 3 |
G | 180≤x<200 | 1 |
合计 | 50 | |
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
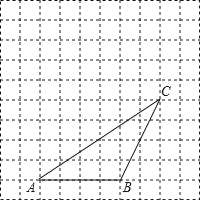
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点(网格线的交点)上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′;
(3)若连接BB′,CC′,则这两条线段的关系是_______;
(4)△ABC的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
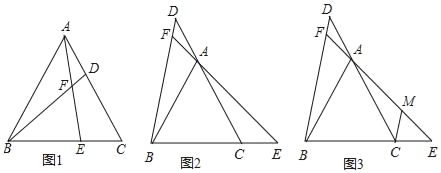
【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为![]() ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,![]() 则:
则:
![]()
(1)填空:![]() ______;
______;
(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”![]() 其中
其中![]() ,
,![]() 且x,均为整数
且x,均为整数![]() ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1 =∠2,∠BAC = 75°将求∠AGD的过程填写完整
解:∵EF∥AD
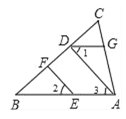
∴ ∠2 = ( )
又∵ ∠1 = ∠2
∴ ∠1 = ∠3。( )
∴AB∥ 。( )
∴∠BAC + = 180°。( )
∵∠BAC=75°∴∠AGD = 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.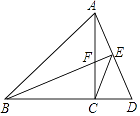
(1)求证:CF=CD;
(2)求证:DADE=DBDC;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种型号的风扇成本分别为120元台、170元台,销售情况如下表所示(成本、售价均保持不变,利润=收入-成本):
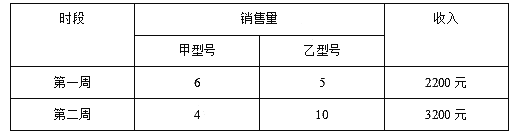
(1)求这两种型号风扇的售价;
(2)该商场打算再采购这两种型号的风扇共130台,销售完后总利润能不能恰好为8010元?若能,给出相应的采购方案;若不能,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com