
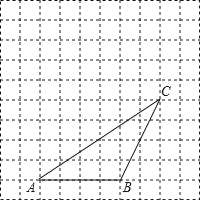
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点(网格线的交点)上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′;
(3)若连接BB′,CC′,则这两条线段的关系是_______;
(4)△ABC的面积为_______.
【答案】(1)见解析;(2)见解析;(3)BB′//CC′,BB′= CC′;(4)8.
【解析】
(1)利用网格特点和平移的性质分别画出点A、B、C的对应点A′、B′、C′即可得到△A′B′C′;(2)连接A′C′为对角线的矩形的另一条对角线,交A′C′于D′,连接B′D′即可;(3)根据平移的性质求解;(4)根据网格特点,利用三角形面积公式计算即可.
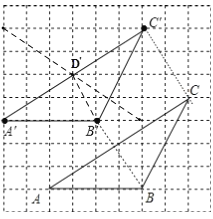
(1)如图,△A′B′C′即为所求;
(2)如图,连接A′C′为对角线的矩形的另一条对角线,交A′C′于D′,连接B′D′,B′D′即为所求;
(3)∵△ABC通过平移得到△A′B′C′,
∴BB′//CC′,BB′= CC′,
(4)S△ABC=![]() ×4×4=8.
×4×4=8.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
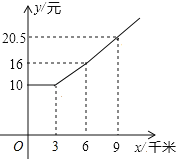
【题目】作为网红城市的重庆,五一节小长假将迎来旅行的高峰,为方便外地游客的出行,重庆市某约车公司推出了一种新型的打车方式,该打车方式的费用收取是按照行驶的路程进行分段计费.小李选用了该打车方式出行,图中折线是小李打车所付车费y(元)与路程x(千米)之间的关系,请根据图象信息,解决下列问题
(1)若小李打车的路程为26千米,则小李所付的车费为 ;
(2)请求出当3≤x≤6时车费y(元)与路程x(千米)之间的关系式;
(3)若小李支付的车费为37元,求小李打车的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A.2种B.3种C.4种D.5种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )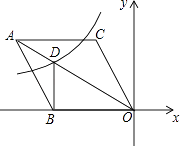
A.6 ![]()
B.﹣6 ![]()
C.12 ![]()
D.﹣12 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
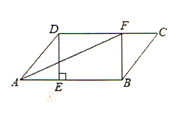
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).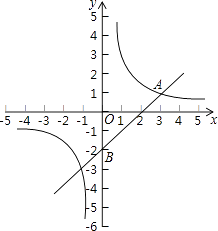
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com