
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).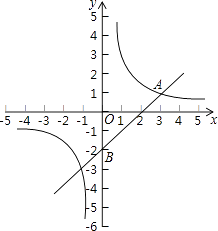
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
【答案】
(1)解:∵反比例函数y= ![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3= ![]()
∴m=3.
∴反比例函数的表达式为y= ![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,﹣2).
∴ ![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为y=x﹣2;
(2)解:令y=0,∴x﹣2=0,x=2,
∴一次函数y=x﹣2的图象与x轴的交点C的坐标为(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+ ![]() PC×2=3.
PC×2=3.
∴PC=2,
∴点P的坐标为(0,0)、(4,0).
【解析】(1)由反比例函数的图象过点A(3,1),求出反比例函数的表达式,由一次函数y=kx+b的图象过点A(3,1)和B(0,﹣2),用待定系数法求出一次函数的表达式;(2)由一次函数y=x﹣2的图象与x轴的交点C的坐标为(2,0),由S△ABP的值,求出PC的值,得到点P的坐标.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )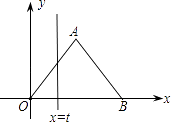
A.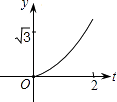
B.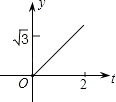
C.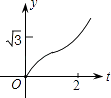
D.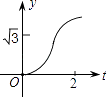
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点(网格线的交点)上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′;
(3)若连接BB′,CC′,则这两条线段的关系是_______;
(4)△ABC的面积为_______.
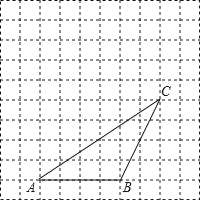
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为![]() ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,![]() 则:
则:
![]()
(1)填空:![]() ______;
______;
(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”![]() 其中
其中![]() ,
,![]() 且x,均为整数
且x,均为整数![]() ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1 =∠2,∠BAC = 75°将求∠AGD的过程填写完整
解:∵EF∥AD
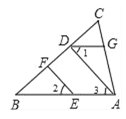
∴ ∠2 = ( )
又∵ ∠1 = ∠2
∴ ∠1 = ∠3。( )
∴AB∥ 。( )
∴∠BAC + = 180°。( )
∵∠BAC=75°∴∠AGD = 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC∥BD,要使△ABC≌△BAD需再补充一个条件,下列条件中,不能选择的是( )
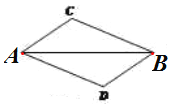
A. BC∥AD B. AC=BD C. BC=AD D. ∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.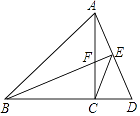
(1)求证:CF=CD;
(2)求证:DADE=DBDC;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,关于此二次函数有以下四个结论:①a<0;②c>0;③b2﹣4ac>0;④ab>0,其中正确的有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
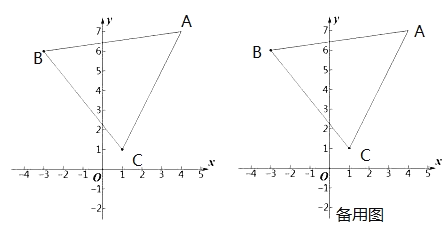
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() 其中
其中![]() 满足:
满足:![]() .
.
(1)![]()
(2)在坐标平面内,将△ABC平移,点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,若平移后E、F两点都在坐标轴上,请直接写出点E的坐标;
(3)若在△ABC内部的![]() 轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com