
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.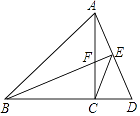
(1)求证:CF=CD;
(2)求证:DADE=DBDC;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
【答案】
(1)证明:∵BE⊥AD,∠ACB=90°,
∴∠CBF=∠CAD=90°﹣∠D,
在△BCF和△ACD中, 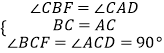 ,
,
∴△BCF≌△ACD,
∴CF=CD;
(2)证明:∵∠FBC=∠CAD,∠D=∠D,
∴△BED∽△ACD,
∴BD:AD=ED:CD,
∴DADE=DBDC;
(3)BE=AE+ ![]() CE,
CE,
证明:作CG⊥CE交BE于G,
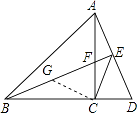
∵∠BEC=45°,
则∠CGE=45°=∠BEC,CG=CE,
∴∠BGC=135°=∠AEC,EG= ![]() CE
CE
在△BCG和△ACE中, 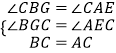 ,
,
∴△BCG≌△ACE,
∴BG=AE,
∴BE=BG+EG=AE+ ![]() CE.
CE.
【解析】(1)根据三角形内角和定理,求出∠CBF=∠CAD,由对应边对应角相等,得到△BCF≌△ACD,根据全等三角形的性质得到对应边CF=CD;(2)根据两角相等得到△BED∽△ACD,得到比例,得到结论DADE=DBDC;(3)根据对应边对应角相等,得到△BCG≌△ACE,得到对应边BG=AE,得出结论BE=BG+EG=AE+![]() CE.
CE.
【考点精析】根据题目的已知条件,利用等腰直角三角形和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
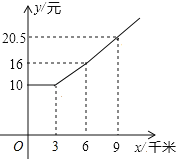
【题目】作为网红城市的重庆,五一节小长假将迎来旅行的高峰,为方便外地游客的出行,重庆市某约车公司推出了一种新型的打车方式,该打车方式的费用收取是按照行驶的路程进行分段计费.小李选用了该打车方式出行,图中折线是小李打车所付车费y(元)与路程x(千米)之间的关系,请根据图象信息,解决下列问题
(1)若小李打车的路程为26千米,则小李所付的车费为 ;
(2)请求出当3≤x≤6时车费y(元)与路程x(千米)之间的关系式;
(3)若小李支付的车费为37元,求小李打车的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
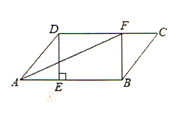
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).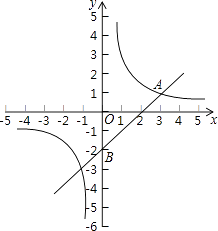
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AD=BE=CF,D、E、F不是各边的中点,AE、BF、CD分别交于P、M、H,如果把三个三角形全等叫做一组全等三角形,那么图中全等三角形有( )
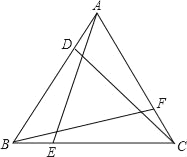
A. 6组 B. 5组 C. 4组 D. 3组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=﹣ ![]() 经( )平移得到y=﹣
经( )平移得到y=﹣ ![]() ﹣1.
﹣1.
A.向右平移2个单位,向上平移1个单位
B.向右平移2个单位,向下平移1个单位
C.向左平移2个单位,向上平移1个单位
D.向左平移2个单位,向下平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
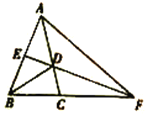
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com