
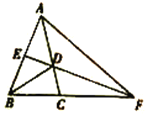
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)依据AB=AC,∠BAC=36°,可得∠ABC=72°,再根据BD是∠ABC的平分线,即可得到∠ABD=36°,由∠BAD=∠ABD,可得AD=BD,依据E是AB的中点,即可得到FE⊥AB;
(2)依据FE⊥AB,AE=BE,可得FE垂直平分AB,进而得出∠BAF=∠ABF,依据∠ABD=∠BAD,即可得到∠FAD=∠FBD=36°,再根据∠AFC=∠ACB﹣∠CAF=36°,可得∠CAF=∠AFC=36°,进而得到AC=CF.
(1)∵AB=AC,∠BAC=36°,∴∠ABC=∠ACB =72°.
又∵BD是∠ABC的平分线,∴∠ABD=∠FBD= 36°,∴∠BAD=∠ABD,∴AD=BD.
又∵E是AB的中点,∴DE⊥AB,即FE⊥AB;
(2)∵FE⊥AB,AE=BE,∴FE垂直平分AB,∴AF=BF,∴∠BAF=∠ABF.
又∵∠ABD=∠BAD,∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,∴∠AFC=∠ACB﹣∠CAF=36°,∴∠CAF=∠AFC=36°,∴AC=CF,即△ACF为等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.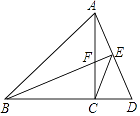
(1)求证:CF=CD;
(2)求证:DADE=DBDC;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种型号的风扇成本分别为120元台、170元台,销售情况如下表所示(成本、售价均保持不变,利润=收入-成本):
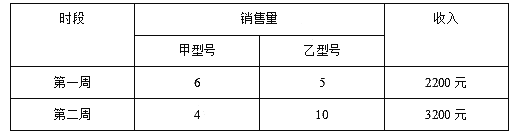
(1)求这两种型号风扇的售价;
(2)该商场打算再采购这两种型号的风扇共130台,销售完后总利润能不能恰好为8010元?若能,给出相应的采购方案;若不能,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
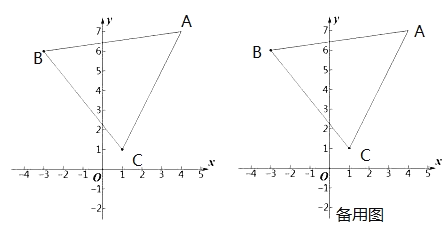
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() 其中
其中![]() 满足:
满足:![]() .
.
(1)![]()
(2)在坐标平面内,将△ABC平移,点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,若平移后E、F两点都在坐标轴上,请直接写出点E的坐标;
(3)若在△ABC内部的![]() 轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是射线BM上的一个动点(点P不与点B重合),∠AOB= 30°,∠ABM=60°.当∠OAP=______时,以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )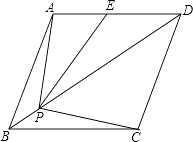
A.![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,DE垂直平分AB ,分别交AB、BC于点D 、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.
(1)如图1,若∠BAC= 100°,求∠EAN的度数;
(2)如图2,若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=a(a≠90°),请直接写出∠EAN的度数. (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com