
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
【答案】应用:解:①若PB=PC,连接PB,则∠PCB=∠PBC, ∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD= ![]() DB=
DB= ![]() AB,
AB,
与已知PD= ![]() AB矛盾,∴PB≠PC,
AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD= ![]() AB,得PD=BD,
AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°;
探究:解:∵BC=5,AB=3,
∴AC= ![]() =
= ![]() =4,
=4,
① 若PB=PC,设PA=x,则x2+32=(4﹣x)2 ,
∴x= ![]() ,即PA=
,即PA= ![]() ,
,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或 ![]() .
.
【解析】应用:连接PA、PB,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数;探究:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.
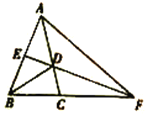
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
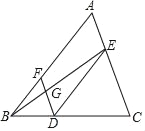
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC关于x轴对称得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)把△A1B1C1平移,使点B1平移到B2(3,4),请作出△A1B1C1平移后的△A2B2C2,并写出A2的坐标;
(3)已知△ABC中有一点D(a,b),求△A2B2C2中的对应点D2的坐标.
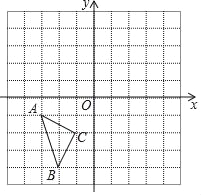
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在线段CD上,AE,BE分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC有怎样的位置关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点A、B、C、D在一条直线上,填写下列空格:
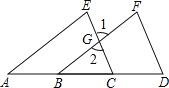
因为∠1=∠E(已知),所以______ // ______ .
因为CE//DF(已知),所以∠1=∠ ______ ,所以∠E=∠ ______ .
(2)说出(1)的推理中应用了哪两个互逆的真命题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com