
����Ŀ������ͼ��ʾ��ֱ������ϵ�У�ÿ��С�����DZ߳�Ϊ1�������Σ���ABC�Ķ�����ڸ���ϣ���A�������ǣ���3����1����
��1������ABC����x��ԳƵõ���A1B1C1��������A1B1C1����д����B1�����ꣻ
��2������A1B1C1ƽ�ƣ�ʹ��B1ƽ�Ƶ�B2��3��4������������A1B1C1ƽ�ƺ����A2B2C2����д��A2�����ꣻ
��3����֪��ABC����һ��D��a��b��������A2B2C2�еĶ�Ӧ��D2�����꣮
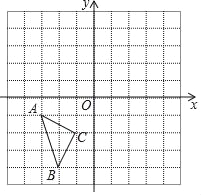
���𰸡���1����ͼ��ʾ����������B1������Ϊ����2��4������2��A2������Ϊ��2��1������3����A2B2C2�еĶ�Ӧ��D2������Ϊ��a+5����b����
��������
(1) �ֱ�������A, B��C����x��Գ� �õ��Ķ�Ӧ��, ��˳�����ӿɵ�;
(2) �ɡ�A1B1C1ƽ�ƣ�ʹ��B1ƽ�Ƶ�B2��3��4��, �ɵ�ƽ�Ƶĵ�λ���ɵ�A2������Ϊ;
(3) ����ƽ��ǰ����������ɿɵ�.
��1����ͼ��ʾ����A1B1C1��Ϊ����B1������Ϊ����2��4����
��2����ͼ��ʾ����A2B2C2��Ϊ����A2������Ϊ��2��1����
��3����A2B2C2�еĶ�Ӧ��D2������Ϊ��a+5����b����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ӳֽ�������������ӣ�ÿ��������3�����β����2���������ε�����ɡ�Ӳֽ������ͼ���ַ�ʽ�ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����档

����19��Ӳֽ�壬�ü�ʱ![]() ����A������������B������
����A������������B������
��1����![]() �Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
��2�����ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳�Ϊ2����ABC=60�㣬E��AD���е㣬��P�ǶԽ���BD�ϵĶ��㣬��AP+PE��ֵ��Сʱ��PC�ij��ǣ� ��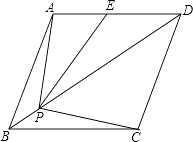
A.![]()
B.2 ![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��y�ķ�����![]() ���������н�����
�������������
��![]() �Ƿ�����Ľ���������aȡ��ֵ��x��y��ֵ�������ܻ�Ϊ�෴����
�Ƿ�����Ľ���������aȡ��ֵ��x��y��ֵ�������ܻ�Ϊ�෴����
����a��1ʱ��������Ľ�Ҳ�Ƿ���x+y��4��a�Ľ�����x��y�Ķ�Ϊ��Ȼ���Ľ���4����
������ȷ�ĸ���Ϊ��������
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ĵĸ�����ǿ��������¸�� ���壺�������ε��������������ȵĵ㣬�����������ε����ģ�
��������ͼ1����PA=PB�����PΪ��ABC�����ģ�
Ӧ�ã���ͼ2��CDΪ�ȱ�������ABC�ĸߣ�����P�ڸ�CD�ϣ���PD= ![]() AB�����APB�Ķ�����
AB�����APB�Ķ�����
̽������֪��ABCΪֱ�������Σ�б��BC=5��AB=3������P��AC���ϣ���̽��PA�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�߳�Ϊ40cm��������Ӳֽ�壬�����ʵ��ļ��ã��۳�һ�������κ��ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ��� 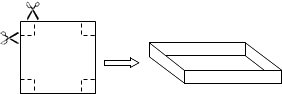
��1����ͼ������������Ӳֽ����ĽǸ���һ��ͬ����С�������Σ���ʣ�ಿ���۳�һ���ǵij����κ��ӣ� ��Ҫʹ�۳ɵij����κ��ӵĵ����Ϊ484cm2 �� ��ô�����������εı߳�Ϊ���٣�
���۳ɵij����κ��ӵIJ�����Ƿ������ֵ������У����������ֵ�ʹ�ʱ�����������εı߳������û�У�˵�����ɣ�
��2������������Ӳֽ������ܼ���һЩ���Σ��������ľ���������һ������������Ӳֽ��ı��ϣ�����ʣ�ಿ���۳�һ���иǵij����κ��ӣ����۳ɵ�һ�������κ��ӵı����Ϊ550cm2 �� ���ʱ�����κ��ӵij��������ߣ�ֻ���������Ҫ���һ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������

�ߡ�1����2(��֪)��
��________��________(__________________________)��
�ߡ�2����3(��֪)��
��________��________(___________________________)��
��________��________(___________________________)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ������������������ȡ��У������Ů�����г���������
��֪��ȡ����������������Ů����������ͬ�������������ݻ�������ͳ��ͼ������A����x<155��B����155��x<160��C����160��x<165��D��165��x<170��E����x��170��
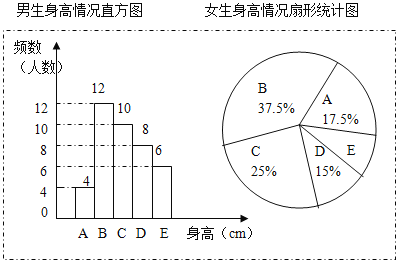
����ͼ���ṩ����Ϣ���ش�����������
��1�������������������������� ��������� ����
��2��������������������E��������� ����
��3����֪��У��������400����Ů��380���������������160��x<170֮���ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�OAB�͵ȱߡ�AFE��һ�߶���x���ϣ�˫����y= ![]() ��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��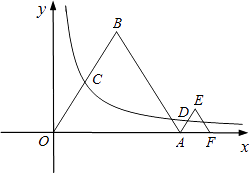
��1�����˫��������ʾ�ĺ�������ʽ��
��2����ȱߡ�AEF�ı߳���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com