
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= ![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.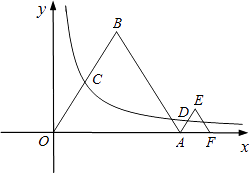
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
【答案】
(1)
解:过点C作CG⊥OA于点G,
∵点C是等边△OAB的边OB的中点,
∴OC=2,∠AOB=60°,
∴OG=1,CG=OGtan60°=1 ![]() =
= ![]() ,
,
∴点C的坐标是(1, ![]() ),
),
由 ![]() =
= ![]() ,得:k=
,得:k= ![]() ,
,
∴该双曲线所表示的函数解析式为y= ![]()

(2)
解:过点D作DH⊥AF于点H,设AH=a,则DH= ![]() a.
a.

∴点D的坐标为(4+a, ![]() a),
a),
∵点D是双曲线y= ![]() 上的点,
上的点,
由xy= ![]() ,得
,得 ![]() a(4+a)=
a(4+a)= ![]() ,
,
即:a2+4a﹣1=0,
解得:a1= ![]() ﹣2,a2=﹣
﹣2,a2=﹣ ![]() ﹣2(舍去),
﹣2(舍去),
∴AD=2AH=2 ![]() ﹣4,
﹣4,
∴等边△AEF的边长是2AD=4 ![]() ﹣8
﹣8
【解析】(1)过点C作CG⊥OA于点G,根据等边三角形的性质求出OG、CG的长度,从而得到点C的坐标,再利用 待定系数法求反比例函数解析式列式计算即可得解;(2)过点D作DH⊥AF于点H,设AH=a,根据等边三角形的性质表示出DH的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到a的值,从而得解.


科目:初中数学 来源: 题型:
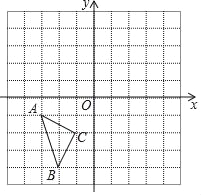
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC关于x轴对称得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)把△A1B1C1平移,使点B1平移到B2(3,4),请作出△A1B1C1平移后的△A2B2C2,并写出A2的坐标;
(3)已知△ABC中有一点D(a,b),求△A2B2C2中的对应点D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华书店推出售书优惠方案:一次性购书不超过100 元,不享受优惠;一次性购书超过100元但不超过200元一律打九折;一次性购书200元以上一律打八折.
(1)如果小明一次性购书的原价为250元,那么他实际付款_________元;
(2)如果小华同学一次性购书付款162元,那么小华所购书的原价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 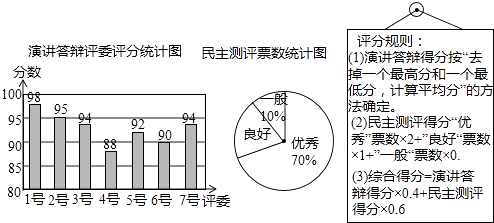
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b,c在数轴上所对应的点分别是A,B.C三点,且a,b满足,①多项式![]() x|a|+(a﹣2)x+7是关于x的二次三项式:②(b﹣1)2+|c﹣5|=0
x|a|+(a﹣2)x+7是关于x的二次三项式:②(b﹣1)2+|c﹣5|=0
(1)请在图1的数轴上描出A,B,C三点,并直接写出a,b,c三数之间的大小关系 用“<”连接);
(2)点P为数轴上C点右侧一点,且点P到A点的距离是到C点距高的2倍,求点P在数轴上所对应的有理数;
(3)点A在数轴上以每秒1个单位长度的速度向左运动,同时点B和点C在数轴上分别以每秒m个单位长度和4个单位长度的速度向右运动(其中m<4),若在整个运动的过程中,点B到点A的距离与点B到点C的距离差始终不变,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: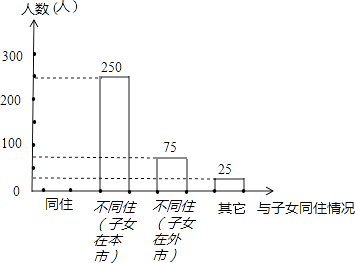
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为a的大正方形,剪去一个边长为b的小正方形,即图①称之为“前世”,然后再剪拼成一个新长方形如图②称之为“今生”,请你解答下面的问题:

(1)“前世”图①的面积与“今生”图②新长方形的面积 ;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为: ,标明“今生”图②新长方形的长为 、宽为 ,面积为: .
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为: .
(4)请你根据(3)题中乘法公式,计算:2.001×1.999.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com