
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

【答案】(1)证明见解析(2)13
【解析】
试题(1)先根据同角的余角相等得到∠ACE=∠BCD,再结合等腰直角三角形的性质即可证得结论;
(2)根据全等三角形的性质可得AE=BD,∠EAC=∠B=45°,即可证得△AED是直角三角形,再利用勾股定理即可求出DE的长.
(1)∵△ACB和△ECD都是等腰直角三角形
∴AC=BC,EC=DC,∠ACB=∠ECD=90°
∵∠ACE=∠DCE-∠DCA,∠BCD=∠ACB-∠DCA
∴∠ACE=∠BCD
∴△ACE≌△BCD(SAS);
(2)∵△ACB和△ECD都是等腰直角三角形
∴∠BAC=∠B=45°
∵△ACE≌△BCD
∴AE=BD=12,∠EAC=∠B=45°
∴∠EAD=∠EAC+∠BAC=90°,
∴△EAD是直角三角形
![]()


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.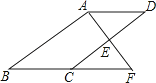
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
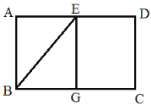
【题目】如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
(1)填空:如图1,当点G恰好在BC边上时,四边形ABGE的形状是___________形;
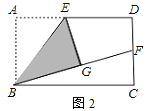
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
![]() 求证:BF=AB+DF;
求证:BF=AB+DF;
![]() 若AD=
若AD=![]() AB,试探索线段DF与FC的数量关系.
AB,试探索线段DF与FC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.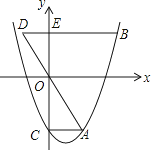
(1)用含m的代数式表示BE的长.
(2)当m= ![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() ,下列结论中,不正确的是( )
,下列结论中,不正确的是( )
A.图象必经过点(1,2)
B.y随x的增大而增大
C.图象在第一、三象限内
D.若x>1,则0<y<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列一元一次方程:
(1)0.5x﹣0.7=6.5﹣1.3x (2)1﹣2(2x+3)=﹣3(2x+1)
(3)5(x+8)=6(2x﹣7)+5; (4)5﹣![]() =x
=x
(5)![]() ﹣
﹣![]() =1 (6)
=1 (6)![]() ﹣
﹣![]() =
=![]() ﹣1.
﹣1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com